Полное приращение и полный дифференциал

Определение. Для функции f(x, y) выражение Dz = f( x + Dx, y + Dy) – f(x, y) называется полным приращением.

Если функция f(x, y) имеет непрерывные частные производные, то

Применим теорему Лагранжа к выражениям, стоящим в квадратных скобках.

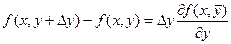
здесь

Тогда получаем

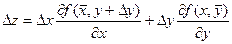
Т.к. частные производные непрерывны, то можно записать равенства:

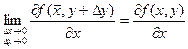
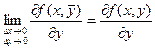
Определение. Выражение 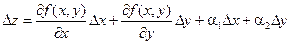называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a₁ и a₂ – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.

Определение: Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).

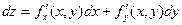
Для функции произвольного числа переменных:

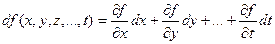
Пример. Найти полный дифференциал функции .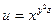

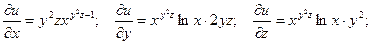
Пример. Найти полный дифференциал функции

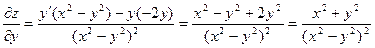
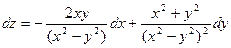
Геометрический смысл полного дифференциала