
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Позиційні системи числення. Переведення числа з однієї системи числення в іншу
Числа, що оброблюються технічними засобами, в першу чергу електронно-обчислювальною машиною (ЕОМ), представляються в них у вигляді спеціальних кодів в прийнятій системі числення.
ЕОМ – це комплекс апаратних, архітектурних та програмних засобів, призначених для автоматичної обробки інформації.
Система числення є сукупністю прийомів позначення (запису) чисел за допомогою знаків. Розрізняють непозиційні та позиційні системи числення. В непозиційних системах числення значення кожного знаку не має чіткої прямої залежності від його положення в числі.
Сучасна позиційна система числення виникла в Індії в V столітті н.е. В позиційній системі числення значення кожної цифри залежить від її позиції (розташування) в числі.
При зображенні чисел в позиційній системі числення розрізняють базу і основу системи.
База – це послідовна сукупність знаків, за допомогою яких записуються числа. Кількість цифр, за допомогою яких записуються числа у даній системі числення, називається основою системи числення. Основа показує у скільки разів одиниця наступного (лівого) розряду більше одиниці попереднього (правого) розряду.
Будь-яке число у позиційній системі числення можна представити у вигляді ряду:
 ,
,
де q – основа системи числення; n – номер розряду; k та m – цілі додатні числа-номери старшого та молодшого розрядів;  – цілі додатні числа від 0 до q-1 (
– цілі додатні числа від 0 до q-1 (  ), що показують скільки одиниць n-го розряду міститься у числі.
), що показують скільки одиниць n-го розряду міститься у числі.
Для людини природнім є запис чисел у десятковій системі числення. Наприклад:
 ,
,
 .
.
Для ЕОМ десяткова система числення не найзручніша. Оскільки для представлення окремих розрядів необхідно мати фізичні елементи, що мають десять різноманітних стійких станів, що дуже важко. Ще складніше реалізувати апаратно виконання арифметичних операцій над даними числами.
Застосування електричної енергії та винахід електронних елементів, що мають два стійких стани (є потенціал або імпульс або нема потенціалу або імпульсу), обумовили широке застосування двійкової системи числення. Будь-яке число в цій системі числення можна позначити за допомогою двох цифр: 1 або 0
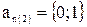 .
.
Окрім десяткової системи числення при обробці інформації також використовуються 8-а та 16-а, а також двійково-десятковий код. 8-а та 16-а системи числення застосовуються для скорочення довжини запису при кодуванні програми та розміщенні даних в пам’яті ЕОМ.
 .
.
 .
.
У якості проміжку між десятковим та двійковим записом використовується двійково-десятковий код. Ряд машин застосовують цей код лише при введенні даних, переводячи його потім у двійкову систему. У таблиці 1.1 представлені числа від 0 до 17 у 10-й, 2-й, 8-й та 16-й системах числення.
Розглянемо переведення чисел із однієї системи числення в іншу.
Таблиця 1.1
Ряд чисел у 10-й, 2-й, 8-й та 16-й системах числення
| q=10 | q=2 | q=8 | q=16 |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Для переведення цілого десятинного числа в систему числення з основою q необхідно поетапно ділити його на основу нової системи числення, поки не отримаємо остаток менше за q. Число в новій системі числення записується у вигляді залишків від ділення на кожному етапі починаючи з останнього.
Наприклад, потрібно перевести число  в 2-у, 8-у та 16-у систему числення:
в 2-у, 8-у та 16-у систему числення:
 .
.
Для переведення десятинних дробів в систему числення з основою q необхідно послідовно помножити дріб на цю основу і виділяти цілі частини числа при кожній операції множення. Множення закінчується, коли черговий добуток стає рівним нулю або при отриманні заданого ступеню точності.


Число в новій системі числення представляється в вигляді послідовності цифр цілих частин добутку.
Наприклад, розглянемо переведення числа  з точністю до чотирьох знаків після коми:
з точністю до чотирьох знаків після коми:



Переведення числа із системи числення з основою q в десятинну виконується наступним чином:

Для переведення з 2-ї в 8-у або 16-у систему числення та навпаки користуються спрощеним прийомом в зв’язку з тим, що числа 8 та 16 відповідно дорівнюють 23 та 24. Для переведення з 2-ї в 8-у (16-у) систему числення достатньо починаючи з десятинної точки цілу та дробову частину числа розбити на тріади (тетради) і кожну тріаду (тетраду) замінити 8-ю (16-ю) цифрою. Переведення 8-х та 16-х чисел в 2-у систему числення здійснюється в зворотному порядку.
Наприклад:
|
|

|
|

Тетрада – 4 розряди
Тріада – 3 розряди
Дата добавления: 2014-12-30; просмотров: 400; Мы поможем в написании вашей работы!; Нарушение авторских прав |