Методи правих та центральних різниць чисельного диференціювання

Приріст аргументу і приріст функції. Нехай функція y = f(x) визначена в точках x₀ та x₁ = x₀ + Δx. Різниця x₁ – x₀ = Δx називається приростом аргументу, а різниця f(x₁) – f(x₀)= f(x₀ + Δx) – f(x₀) називається приростом функції при переході від значення аргументу x₀ до аргументу x₁ = x₀ + Δx. Приріст функції позначається Δf або Δy, тобто Δf = f(x₀ + Δx) – f(x₀).

Похідною функції f(x) в точці x₀ (позначають f'(x₀)) називається межа відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, тобто

,

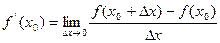де Δx = x₁ – x₀ – приріст аргументу; x₁ і x₀ – два значення незалежної змінної з області визначення функції f(x); f(x₀ + Δx) – f(x₀) = Δf – приріст функції в точці x₀.

Наприклад, якщо f(x)= 3x² + 2, то f'(x₀) =

= =

= .

Функція, яка має похідну в точці x₀, називається такою, що диференціюється в цій точці. Якщо функція має похідну в кожній точці деякого проміжку, то вона диференційована на цьому проміжку. Похідна функції f(x), що диференціюється на проміжку, сама є функцією аргументу x.

Похідна широко використовується в різних методах аналізу даних, причому від ефективності обчислення похідної залежить ефективність, а часто і сама можливість реалізації вживаних методів аналізу. Похідні можуть визначатися аналітично або чисельно.

Кінцево-різницеві схеми чисельного визначення похідних побудовані на ідеї застосування такого малого приросту аргументу (похитування), що обчислення дає достатню для практичного застосування точність. Формула методу правих різниць є класичною формулою визначення похідної і виглядає наступним чином:

,

а метод центральних різниць може бути записаний як

,

де в обох випадках h – кінцево-різницевий інтервал (крок похитування).

Крок похитування h повинен наближуватись до нуля (дорівнює маленькій величині).

Наведемо фрагмент програми чисельного диференціювання.

#include <iostream>

using namespace std;

double func(double x)

{

return x*x + 5*x + 6;

}

void main()

{

double x,h,t1,t2;

h = 0.0000000001;

x = 3;

t1 = (func(x+h)-func(x))/h;

t2 = (func(x+h)-func(x-h))/(2*h);

cout<<"\nПохідна (метод правих різниць) "<<t1;

cout<<"\nПохідна (метод центральних різниць) "<<t2;

}

У даному фрагменті на прикладі функції y = x² + 5x + 6 реалізовано методи правих та центральних різниць, відповідно змінні t1 та t2. Результат виконання програми при значенні аргументу x = 3 виглядатиме наступним чином:

Похідна (метод правих різниць) 11

Похідна (метод центральних різниць) 11