
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сортування Шелла
Сортування Шелла називається так на ім’я свого автора, Дональда Л. Шелла (відкрите в 1959 р.). Проте ця назва закріпилася тому, що дія цього методу часто ілюструється рядами морських раковин, які перекривають одна одну (по-англійськи «shell» - «раковина»). Загальна ідея запозичена з сортування вставками і ґрунтується на зменшенні кроків (крок – це відстань між сортованими елементами на конкретному етапі сортування). Розглянемо діаграму (рис. 15.1). Спочатку сортуються всі елементи, віддалені один від одного на три позиції. Потім сортуються елементи, розташовані на відстані двох позицій. Нарешті, сортуються всі сусідні елементи.
Те, що цей метод дає гарні результати, або навіть те, що він взагалі сортує масив, побачити не так просто. Проте, це вірно. Кожен прохід сортування розповсюджується на відносно невелику кількість елементів або на елементи, розташовані вже у відносному порядку. Тому сортування Шелла ефективне, а кожен прохід підвищує впорядкованість, тобто зменшує кількість безладів (інверсій).
Конкретна послідовність кроків може бути і інша. Єдине правило полягає в тому, щоб останній крок був рівний 1. Наприклад, така послідовність: 9, 5, 3, 2, 1 дає ефективні результати і застосовується у показаній тут реалізації сортування Шелла. Слід уникати послідовностей, які є ступенями числа 2 – по математично складних міркуваннях вони зменшують ефективність сортування (але сортування буде працювати).
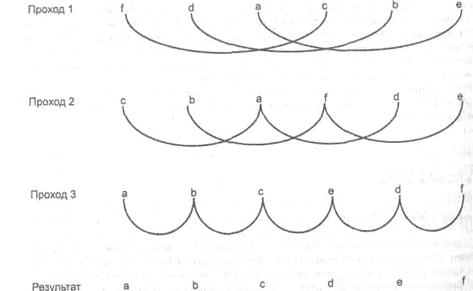
Рис.15.1 Сортування Шелла
void ShellSort(double* items, int l, int r)
{
int i,j,gap,k;
double x,a[5];
a[0]=9;a[1]=5;a[2]=3;a[3]=2; a[4]=1;
for(k=0;k<5;k++)
{
gap=a[k];
for(i=gap;i<=r;i++)
{
x=items[i];
for(j=i-gap;(x<items[j]) && (j>=l);j-=gap)
items[j+gap]=items[j];
items[j+gap]=x;
}
}
}
Аналіз сортування Шелла пов’язаний з дуже складними математичними задачами. Час сортування пропорційний п1,2 при сортуванні п елементів. А це вже істотне поліпшення в порівнянні з сортуваннями порядку п2. Проте, алгоритм швидкого сортування ще ефективніший.
15.5. Швидке сортування (quick sort)
Швидке сортування, придумане Ч. А. Р. Хоаром (Charles Antony Richard Hoare) і названо його ім’ям, вважається кращим з існуючих в даний час алгоритмів сортування загального призначення. У його основі лежить сортування обмінами.
Швидке сортування побудоване на ідеї ділення. Загальна процедура полягає в тому, щоб вибрати деяке значення, назване компарандом (comparand, операнд в операції порівняння, іноді називається також основою або критерієм розбиття), а потім розбити масив на дві частини. Всі елементи, більші або рівні компаранду, переміщаються на одну сторону, а менші – на іншу. Потім цей процес повторюється для кожної частини до тих пір, поки масив не буде відсортований. Наприклад, якщо початковий масив складається з чисел 6, 5, 4, 1, 3, 2, а у якості компаранди використовується число 4, перший прохід швидкого сортування переупорядкує масив таким чином:
Початок 6 5 4 1 3 2
Прохід 1 2 3 1 4 5 6
Потім сортування повторюється для обох половин масиву, тобто 2 3 1 і 4 5 6. Як видно, цей процес за своєю суттю рекурсивний, і, дійсно, в чистому вигляді швидке сортування реалізується як рекурсивна функція.
Значення компаранди можна вибирати двома способами – випадковим чином або усереднивши невелику кількість значень з масиву. Для оптимального сортування необхідно вибирати значення, яке розташоване точно у середині діапазону всіх значень. Проте для більшості наборів даних це зробити непросто. У гіршому разі вибране значення виявляється одним з крайніх. Проте, навіть в цьому випадку швидке сортування працює правильно. У приведеній нижче версії швидкого сортування у якості компаранди вибирається середній елемент масиву.
void QuickSort(double * items, int l, int r)
{
int i,j;
double x,y;
i=l;j=r;
x=items[(l+r)/2];
do
{
while((items[i]<x) && (i<r)) i++;
while((x<items[j]) && (j>l)) j--;
if(i<=j)
{
y=items[i];
items[i]=items[j];
items[j]=y;
i++;j--;
}
}while(i<=j);
if(l<j) QuickSort(items,l,j);
if(i<r) QuickSort(items,i,r);
}
Середня кількість порівнянь дорівнює n log n, а середня кількість обмінів приблизно рівна n/6 log n. Ці величини набагато менше відповідних характеристик розглянутих раніше алгоритмів сортування.
Необхідно згадати про один особливо проблематичний аспект швидкого сортування. Якщо значення компаранди в кожному діленні дорівнює найбільшому значенню, швидке сортування стає «повільним сортуванням» з часом виконання порядку n2. Тому треба уважно вибрати метод визначення компаранди. Цей метод часто визначається природою сортованих даних. Наприклад, в дуже великих списках поштової розсилки, в яких сортування відбувається по поштовому індексу, вибір простий, тому що поштові індекси досить рівномірно розподілені – компаранду можна визначити за допомогою простої функції алгебри. Проте в інших базах даних часто кращим вибором є випадкове значення.
Кожен програміст повинен мати в своєму розпорядженні широкий набір алгоритмів сортування. Не дивлячись на те, що в середньому випадку оптимальним є саме швидке сортування, воно не є кращим у всіх випадках. Наприклад, при сортуванні дуже маленьких списків (наприклад, менше 100 елементів) додатковий об’єм роботи створюваний рекурсивними викликами швидкого сортування, може перекрити переваги її більш ефективного алгоритму. У таких окремих випадках один з простих методів сортування – можливо, навіть бульбашкове сортування – може працювати швидше. Крім того, якщо відомо, що список вже майже впорядкований або якщо немає потреби переставляти однакові елементи, який-небудь інший алгоритм підійде краще ніж швидке сортування. Швидке сортування є кращим алгоритмом загального призначення, але це не означає що в конкретних випадках інші підходи не дадуть кращих результатів.
Наведемо порівняльну таблицю алгоритмів сортування (табл. 15.1). Порівняння методів сортування виконувалась на окремому персональному комп’ютері, тому час виконання кожного з алгоритмів вказаних в таблиці слід розглядати як відносну величину, тобто тільки для порівняння швидкодії та ефективності алгоритмів між собою.
Таблиця 15.1
Час порівняння методів сортування в залежності від кількості елементів масиву
| Метод сортування | Час (секунди) для відповідної кількості елементів | ||
| бульбашкове | 9,078 | 37,25 | 152,094 |
| вибором | 3,796 | 15,625 | 64,25 |
| вставками | 1,969 | 8,562 | 45,079 |
| Шелла | 0,437 | 2,922 | 33,375 |
| швидке | 0,007 | 0,015 | 0,031 |
Найефективнішим алгоритмом сортування серед усіх методів є алгоритм швидкого сортування (quick sort); серед типових алгоритмів сортування – алгоритм вставками (insert sort).
Контрольні питання
1. Які методи сортування масивів ви знаєте?
2. Розкрийте сутність бульбашкового методу сортування. Наведіть приклад.
3. Розкрийте сутність методу сортування за дпомогою вибору. Наведіть приклад.
4. Розкрийте сутність методу сортування вставками. Наведіть приклад.
5. Розкрийте сутність методу сортування Шелла. Наведіть приклад.
6. Розкрийте сутність методу швидкого сортування. Наведіть приклад.
Дата добавления: 2014-12-30; просмотров: 988; Мы поможем в написании вашей работы!; Нарушение авторских прав |