Лінійні дії над матрицями. Множення матриць. Обернена матриця.

Під лінійними діями розуміють додавання і віднімання матриць, множення матриць на скаляр (const). Операція + (–) визначається тільки для матриць однакових розмірів. Сумою (різницею) двох матриць A і B розміром m_xn називається матриця C такого ж розміру у якій елементи обчислюються за формулою 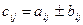. Наприклад C = A – B, де

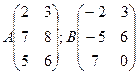
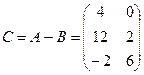
Нульова матриця при + (–) матриць виконує роль звичайного нуля при + (–) чисел. .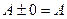

Добутком матриці A на λ (λ = const) називається матриця B, яка отримується з даної помноженням усіх її елементів на скаляр λ.

Помноження матриць відбувається тільки тоді, коли матриця A погоджена з матрицею B (кількість стовпців матриці A дорівнює кількості рядків матриці B).

Тільки квадратні матриці одного порядку є взаємопогоджені. Правило погодження матриць називається правило "рядок на стовбець". Якщо для матриць A і B знайдені добутки A*B і B*A то це не значить, що A*B = B*A. При помноженні квадратної матриці на нульову матрицю отримують нульову матрицю.

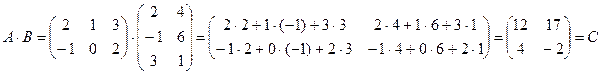
Якщо A і B квадратні матриці одного порядку з визначниками |A| і |B|, то для матриці C = A*B, її визначник |C| = |A*B| = |A| * |B|.

Розглянемо квадратну матрицю n-го порядку. Квадратна матриця A^-1 називається оберненою для квадратної матриці A того ж порядку, якщо виконується рівність .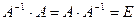

Для того, щоб квадратна матриця A мала обернену, необхідно і достатньо щоб матриця A була невиродженою, тобто щоб її визначник був відмінний від нуля. .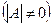

Формула оберненою матриці.

,

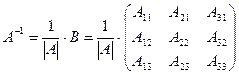де матриця B – транспонована матриця A, у якій елементи замінені алгебраїчними доповненнями.

Необхідною перевіркою правильності знаходження оберненої матриці є рівність .

З точки зору обчислення оберненої матриці – обчислення за допомогою приведеної формули є неоптимальним варіантом, так як при цьому необхідно обчислити n² алгебраїчних доповнень (визначників порядку n-1), а це займає досить багато часу. Одним з самих швидких методів обчислення оберненої матриці є метод Жордана-Гауса, який зводиться до вирішення системи лінійних рівнянь.

Позначимо елементи оберненої матриці через α_lm. Тоді співвідношення AA^-1 = E можна записати так:

.

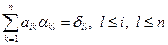Якщо розглядати l-й стовпець оберненої матриці як вектор, то він є вирішенням лінійної системи з матрицею A і спеціальною правою частиною (у якій на l-м місці знаходиться одиниця, а на останніх – нулі).

Таким чином, для обернення матриці треба розв’язати n систем лінійних рівнянь з однаковою матрицею A і різними правими частинами. Приведення матриці A до трикутної форми робиться при цьому тільки один раз.

Цікаво відзначити, що обернення матриці зводиться до вирішення n систем лінійних рівнянь, і вимагає лише втричі більше дій ніж вирішення однієї системи рівнянь. Це пояснюється тим, що при вирішенні лінійної системи велика частина обчислень пов'язана з приведенням матриці до трикутного виду, що при оберненні матриці робиться тільки один раз. Зворотний хід і перетворення правих частин виконуються набагато швидше. Тому, якщо потрібно кілька разів розв’язати лінійну систему з однією і тією ж матрицею, то вигідно привести матрицю до трикутної форми лише один раз.

Наведемо код функцій множення матриць та оберненої матриці методом Жордана-Гауса.

#include <iostream>

#include <cmath>

using namespace std;

# define delta 0.00000001

// Ф-я множення 2-х матриць

// Вход:

/*

m1 – масив-шнурок представлення 1-ї матриці розмірності m*n

m2 – масив шнурок представлення 2-ї матриці розмірності n*l

Обов’язкова умова 2-х вхідних матриць (кількість стовбців 1-ї = кількості рядків 2-ї)

m, n, l – розмірності відповідних матриць

*/

// Вихід m3 – отримана матриця (у вигляді масиву)

// розмірністю m*l елементів

void mumnog(double*m1, double*m2,

int m, int n, int l, double*m3)

{

int i,j,k;

for(i=0;i<m;i++)

for(j=0;j<l;j++)

{

m3[i*l+j] = 0;

for(k=0;k<n;k++)

m3[i*l+j]+=m1[i*n+k]*m2[k*l+j];

}

}

/*

Ф-я знаходження оберненої матриці порядку n методом Гаусса

k - масив входу (матриця A)

bb - масив виходу (матриця A^-1)

*/

bool mObr_Gauss(double*k,double*bb,int n)

{

int i,j,tt,xx,r,kol_el;

double t,vv;

kol_el = n*n;

//Якщо визначник 0 - оберненої матриці не існує.

if(fabs(mopred(k,n))<delta)return false;

double*aa = new double[kol_el];

double*kk = new double[kol_el];

//Перегонка масивів

for(i=0;i<kol_el;i++)

{

aa[i] = 0;

kk[i] = k[i];

}

//Заповнення 1 по головній діагоналі –

//aa - одинична матриця

for(i=0;i<n;i++)aa[i*n+i]=1;

//Приведення нижнього трикутника до нульових

//коефіцієнтів (методом Гауса)

//Маніпуляції виконуються як з поточною,

//так і з одиничною матрицею

for(j=0;j<n;j++)

for(i=n-1;i>j;i--)

{

if (fabs(kk[(i-1)*n+j])<delta)

{

for(xx=j;xx<n;xx++)

{

vv = kk[i*n+xx];

kk[i*n+xx]=kk[(i-1)*n+xx];

kk[(i-1)*n+xx] = vv;

}

for(tt=0;tt<n;tt++)

{

vv = aa[i+tt*n];

aa[i+tt*n] = aa[i+tt*n-1];

aa[i+tt*n-1] = vv;

}

continue;

}//endif

if (fabs(kk[i*n+j])<delta)continue;

t = kk[i*n+j]/kk[(i-1)*n+j];

for(r=j;r<=n;r++)

kk[i*n+r]=kk[i*n+r]-kk[(i-1)*n+r]*t;

for(tt=0;tt<n;tt++)

aa[i+tt*n]=aa[i+tt*n]-aa[i+tt*n-1]*t;

}

//Для кожного стовбця зміненої одиничної матриці

//знаходиться розв’язок

//Таким чином отримуємо обернену матрицю,

//тобто коли A->E, E->A^(-1)

for (i=n-1;i>=0;i--)

{

for (j=n-1;j>i;j--)

for(tt=0;tt<n;tt++)

aa[i+tt*n]-=kk[i*n+j]*aa[j+tt*n];

for(tt=0;tt<n;tt++)

aa[i+tt*n]/=kk[i*n+i];

}

//Запис вихідного масиву(транспонований вид)

for(i=0;i<kol_el;i++)bb[i] = aa[(i%n)*n + i/n];

delete[]aa;

delete[]kk;

return true;

}

Широкого поширення набули прямі чисельні методи розв’язання системи лінійних алгебраїчних рівнянь: оберненої матриці, Крамера, Гауса. Розв’яжемо систему лінійних рівнянь:

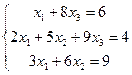
кожним з цих методів.