Метод оберненої матриці.

Одним з прямих методів розв’язання системи лінійних рівнянь є метод оберненої матриці. Розглянемо систему n лінійних рівнянь з n невідомими. Складемо матрицю системи із коефіцієнтів при невідомих і матриці-стовбці невідомих і вільних членів:

, , .

Представимо задану систему в еквівалентному матричному вигляді.

Помножимо обидві частини даного рівняння на обернену матрицю (A^-1), вважаючи, що матриця системи A невироджена .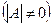

, , – розв’язок матричного рівняння і початкової системи.

Приведемо фрагмент вирішення системи лінійних рівнянь матричним способом.

…………………………………………………………………

void main()

{

double k[9]={

1, 0, 8,

2, 5, 9,

3, 6, 0

};

double cc[9],dd[3];

double aaa[3]={6, 4, 9};

mObr_Gauss(k,cc,3);

mumnog(cc, aaa, 3, 3, 1, dd);

cout<<"\n\n"<<cc[0]<<"\t"<<cc[1]<<"\t"<<cc[2];

cout<<"\n"<<cc[3]<<"\t"<<cc[4]<<"\t"<<cc[5];

cout<<"\n"<<cc[6]<<"\t"<<cc[7]<<"\t"<<cc[8];

cout<<"\n\nx1="<<dd[0]<<"\tx2="<<dd[1]

<<"\tx3="<<dd[2];

}

…………………………………………………………………

У результаті виконання програми, використовуючи функції mObr_Gauss() для обчислення оберненої матриці, та функції mumnog() для множення матриць знайдено обернену матрицю (сс) та корені рівняння (dd):

0.692308 -0.615385 0.512821

-0.346154 0.307692 -0.0897436

0.0384615 0.0769231 -0.0641026

x1 = 6.30769 x2 = -1.65385 x3 = -0.0384615