Метод Крамера

Розглянемо систему n лінійних рівнянь з n невідомими.

будемо називати визначником системи.

Нехай :

Якщо визначник системи ∆ відмінний від нуля то ця система має лише один розв’язок, який знаходять по наступним формулам:

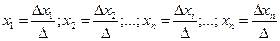
∆x_i – це визначник системи, у якому необхідно замінити коефіцієнти, що стоять попереду невідомого x_i на стовбець вільних членів.

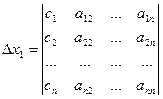
Наведемо фрагмент реалізації системи лінійних рівнянь з 3-ма невідомими методом Крамера.

…………………………………………………………………

void main()

{

double d,dx1,dx2,dx3,x1,x2,x3;

double k[9]={

1,0,8,

2,5,9,

3,6,0

};

/*

double aaa[3]={

6,

4,

};

*/

double aax1[9]={

6,0,8,

4,5,9,

9,6,0

};

double aax2[9]={

1,6,8,

2,4,9,

3,9,0

};

double aax3[9]={

1,0,6,

2,5,4,

3,6,9

};

d = mopred(k, 3);

dx1 = mopred(aax1, 3);

dx2 = mopred(aax2, 3);

dx3 = mopred(aax3, 3);

x1 = dx1/d;

x2 = dx2/d;

x3 = dx3/d;

cout<<"\nx1="<<x1<<"\tx2="<<x2<<"\tx3="<<x3;

}

…………………………………………………………………

У результаті виконання програми, будуть виведені наступні результати:

x1 = 6.30769 x2 = -1.65385 x3 = -0.0384615