Сопротивление цепи RС в комплексной (символической) форме

При рассмотрении сопротивления цепи RL в комплексной форме в предыдущем вопросе был сделан вывод о том, что в комплексной форме при последовательном соединении сопротивления участков просто складываются. Исходя из этого, для цепи RC:

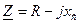
Это можно доказать:

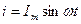
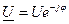
Вывод (к вопросам 33 – 34): модуль комплексного сопротивления есть полное сопротивление цепи Z. Действительная часть — активное (резистивное) сопротивление R, мнимая часть — реактивное сопротивление (x_L или x_c). Аргумент — угол — угол сдвига фаз между напряжением и током.

Вопрос 35. Неразветвлённая RLC электрическая цепь при гармоническом воздействии. Закон Ома. Энергетический процесс. Векторные диаграммы. Входное сопротивление цепи в комплексной форме.

Пусть ток изменяется по закону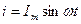

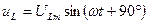
Это справедливо для мгновенных, векторных и комплексных значений.

Возьмём случай:

— реактивная составляющая напряжения

— полное сопротивление цепи RLC

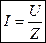— закон Ома для цепи RLC

Разделим все стороны диаграммы напряжений на ток, получим диаграмму сопротивлений (стрелки уже не ставятся):

— реактивное сопротивление цепи RLC

Если , то — цепь носит индуктивный характер.

Если , то — цепь носит емкостной характер.

Умножим все стороны треугольника напряжений на ток, получим треугольник мощностей:

Построим векторную диаграмму напряжений, когда :

Запишем сопротивление цепи в комплексной (символической) форме:

Вопрос 36. Параллельные RL и RC цепи при гармоническом воздействии. Закон Ома. Векторные диаграммы токов. Проводимости. Входное сопротивление цепи в комплексной форме.