Интегрирующее (идеальное) звено.

Уравнение и передаточная функция звена:

или

В случае интегрирующего звена параметр k является коэффициентом передачи звена по скорости, численно равным скорости изменения выходной величины при единичном значении входной величины.

Частотные и временные функции звена:

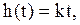
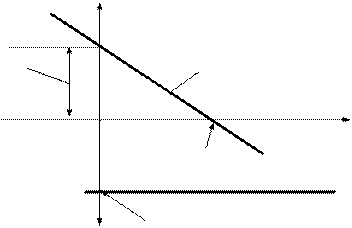
Построенные по указанным функциям характеристики звена представлены на рис.2.12.

При построении ЛАЧХ удобно отложить точку с координатами (при этом ); и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении получаем при увеличении частоты на одну декаду, т.е. при , соответственно Разность этих ординат составляет минус 20 дБ).

В качестве примера элемента, характеристики которого приближенно соответствуют характеристикам идеального интегрирующего звена, можно назвать двигатель постоянного тока с независимым возбуждением и малой электромеханической инерцией. Входной величиной для него является напряжение на зажимах якоря, а выходной - угол поворота вала.

Схема на рис.2.6, б будет являться интегрирующим звеном, если , а цепь обратной связи организована конденсатором, т.е.

На самом деле, согласно формуле (2.5) передаточная функция схемы будет

где

+j АФЧХ А(w)

0 +1

w®¥ 0 w

G(w)

20lgk -20дБ/дек

0 lgw

lgk

j(w)

h(t) w(t)

k

0 t 0 t

Рис.2.12

При использовании в рассматриваемой схеме реального операционного усилителя переходная характеристика не может иметь значения, превышающие напряжение питания. Но если предположить операционный усилитель идеальным, то и реализованное здесь интегрирующее звено будет идеальным.

Дифференцирующее (идеальное) звено.

Уравнение и передаточная функции звена:

Выходная величина пропорциональна скорости изменения входной величины.

Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена.

Выражение для основных функций:

Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена обратны передаточной функции и соответствующим характеристикам интегрирующего звена.

О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить скачок выходной величины бесконечной амплитуды.

Реальные дифференцирующие звенья обладают конечной инерционностью, вследствие чего осуществляемое ими дифференцирование не является точным. Примером может служить тахогенератор, если за его входную величину принять угол поворота его вала, а за выходную величину - выходное напряжение. Последние пропорционально угловой скорости вращения вала, которая в свою очередь равна производной от угла поворота.

Логарифмические частотные характеристики рассматриваемого звена приведены на рис.2.13.

При построении ЛАЧХ удобно отложить точку с координатами w=1 (при этом lgw=0); и провести через нее прямую с наклоном плюс 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ увеличивается на 20 дБ.

G(w)

+20дБ/дек

20lgk

0 lgw

j(w)

Рис.2.13

Апериодическое (первого порядка) звено.

Описывается дифференциальным уравнением

Перейдя к изображениям, получим:

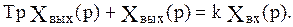
Передаточные и частотные функции:

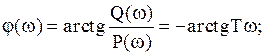
ЛАЧХ звена показано на рис.2.14. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при w®0 и w®¥.

G(w) асимптотическая ЛАЧХ

20lgk -20дБ/дек

точная ЛАЧХ

lgw

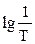
j(w)

Рис.2.14

При малых значениях w можно считать , то есть , следовательно

Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20 lgk. Это есть первая асимптота, к которой стремится ЛАЧХ при w®0.

С другой стороны, на больших частотах

В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении w на декаду, т.е. в 10 раз,

Таким образом, величина уменьшилась на 20 lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при w®¥. Обе асимптоты пересекаются в точке, соответствующей частоте Поэтому эта частота называется сопрягающей частотой.

Максимальное расхождение между точной ( 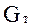) и асимптотической ( 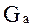) ЛАЧХ наблюдается при частоте, равной сопрягающей.

Вычислим это расхождение, подставив в соотношения для 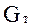и 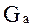значения сопрягающей частоты :

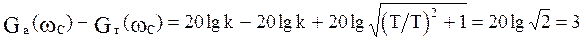дБ.

От параметров звена рассматриваемая величина не зависит.

На этом же рисунке показана и ЛФЧХ: при w®¥ значение j изменяется от 0 до минус . При этом в точке имеем .

АФЧХ представляет собой полуокружность с радиусом в четвертом квадранте комплексной плоскости и центром в точке ( , j0) на действительной оси.

Переходная функция, согласно решению уравнения звена, при и нулевых начальных условиях имеет вид

а импульсная переходная функция

Переходная характеристика представлена на рис.2.15.

h(t)

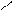k

0 T t

Рис.2.15

Динамические свойства звена характеризуются постоянной времени Т. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

Коэффициент передачи k определяет свойства звена в установившемся режиме.

Очевидно, имея в распоряжении частотные либо переходные характеристики, полученные, например, экспериментально, можно восстановить передаточную функцию звена.

В рассмотренных выше примерах по определению передаточных функций схемы на рис.2.2; рис.2.3; рис.2.6, а являются апериодическими звеньями.