Кодирование вещественных чисел

Существуют два способа представления вещественных чисел в памяти компьютера: с фиксированной точкой и с плавающей точкой.

При представлении вещественных чисел в форме с фиксированной точкой положение десятичной точки в машинном слове фиксировано, например (рис. 2):

Рис.2. Вещественное число с фиксированной точкой.

Чаще всего точка фиксируется перед первым разрядом числа (рис.3).

Рис.3. Вещественное число с точкой перед первым разрядом.

Целое число является частным случаем числа с фиксированной точкой, когда точка фиксирована после последнего разряда.

В форме с плавающей точкой вещественное число х представляется в виде

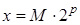
где и называется мантиссой, p – целое число, называемой порядком (рис.4).

Рис. 4. Вещественное число с плавающей точкой.

Количество позиций, отводимых для мантиссы, определяет точность представления чисел, а количество позиций, отводимых для порядка – диапазон представления чисел.

Обычно мантисса записывается в нормализованном виде, то есть так, чтобы отсутствовали незначащие нули в старших разрядах:

0.0011101 ненормализованное представление,

0.1110100 нормализованное представление.

При сложении чисел в форме с плавающей точкой в общем случае нельзя складывать их мантиссы. Если слагаемые имеют разные порядки, то одинаковые разряды мантиссы будут на самом деле изображать разные разряды числа, например:

0.27×10³ и 0.31×10²

При сложении чисел необходимо предварительно выровнять их порядки, то есть числу с меньшим порядком приписать порядок второго числа и соответствующим образом изменить мантиссу, например:

0.31×10² = 0.031×10³.