
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные формулы. · Молярные теплоёмкости при постоянном объёме ( ) и постоянном давлении ( ):
· Молярные теплоёмкости при постоянном объёме ( 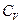 ) и постоянном давлении (
) и постоянном давлении (  ):
):

 ,
,
где  – число степеней свободы,
– число степеней свободы,  - универсальная газовая постоянная.
- универсальная газовая постоянная.
· Связь между удельной ( 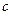 ) и молярной (
) и молярной (  ) теплоёмкостями:
) теплоёмкостями:
 ,
,
где  – молярная масса.
– молярная масса.
· Внутренняя энергия идеального газа:
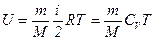 ,
,
где  - масса газа,
- масса газа, 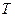 - абсолютная температура.
- абсолютная температура.
· Изменение внутренней энергии идеального газа:
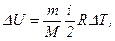
· Работа расширения газа:
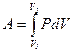 - в общем случае,
- в общем случае,
где  - давление газа,
- давление газа, 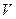 - объём газа.
- объём газа.
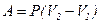 - при изобарном процессе.
- при изобарном процессе.
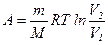 - при изотермическом процессе.
- при изотермическом процессе.
 - при адиабатном процессе,
- при адиабатном процессе,
где  .
.
· Первое начало термодинамики:
 ,
,
где  – количество теплоты, сообщённое системе,
– количество теплоты, сообщённое системе,  - изменение внутренней энергии системы,
- изменение внутренней энергии системы,  – работа, совершённая системой против внешних сил.
– работа, совершённая системой против внешних сил.
· Уравнение Пуассона для адиабатного процесса:
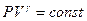 .
.
· Уравнение адиабаты идеального газа в переменных 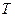 и
и 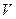
 .
.
· Коэффициент полезного действия цикла Карно:
 ,
,
где  - количество теплоты, полученное от нагревателя,
- количество теплоты, полученное от нагревателя,  - количество теплоты, переданное холодильнику,
- количество теплоты, переданное холодильнику, 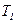 - температура нагревателя,
- температура нагревателя,  - температура холодильника.
- температура холодильника.
Примеры решения задач
Задача 1. Кислород, занимающий при давлении Р=105 Па объем V = 0,04 м3, расширяется так, что объем увеличивается в два раза. Определите конечное давление и работу, совершенную газом при изобарном, изотермическом и адиабатном процессах.
| Дано: Р = 10 5 Па; V = 0,04 м3; V1 =2V =0,08 м3. | Решение
1. При изобарном процессе Р=const, следовательно, Р1=Р=105 Па. Работа при изобарном процессе А1=РΔV=105  (0,08м3–0,04м3)=0,4·104Дж.
2. При изотермическом процессе начальные и конечные значения давления и объема связаны между собой выражением РV=P2V1, откуда: (0,08м3–0,04м3)=0,4·104Дж.
2. При изотермическом процессе начальные и конечные значения давления и объема связаны между собой выражением РV=P2V1, откуда: 
|
| P1 - ? P2 - ? P3 - ? A1 - ? A2 - ? A3 - ? |
Для определения работы газа при изотермическом процессе воспользуемся выражением 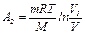 . Из уравнения Клапейрона-Менделеева
. Из уравнения Клапейрона-Менделеева  , следовательно
, следовательно 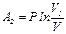 . После подстановки числовых значений и вычисления получаем:
. После подстановки числовых значений и вычисления получаем:  .
.
3. При адиабатном процессе давление и объем связаны между собой уравнением Пуассона: 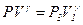 , где
, где  -молярная теплоемкость газа при постоянном давлении,
-молярная теплоемкость газа при постоянном давлении,  - молярная теплоемкость газа при постоянном объеме. Так как молекула кислорода состоит из двух атомов, то
- молярная теплоемкость газа при постоянном объеме. Так как молекула кислорода состоит из двух атомов, то  , а отношение
, а отношение 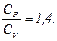 Из уравнения Пуассона:
Из уравнения Пуассона:  . После подстановки и вычисления, получаем:
. После подстановки и вычисления, получаем: 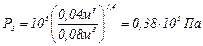 . Работа, совершаемая газом при адиабатном расширении, равна убыли внутренней энергии, т.е.
. Работа, совершаемая газом при адиабатном расширении, равна убыли внутренней энергии, т.е.  , где Т3 – абсолютная температура газа после адиабатного расширения. Запишем уравнение состояния до и после адиабатного расширения газа:
, где Т3 – абсолютная температура газа после адиабатного расширения. Запишем уравнение состояния до и после адиабатного расширения газа:  и
и  , где Т3 – абсолютная температура газа после адиабатного расширения. Из последних двух уравнений:
, где Т3 – абсолютная температура газа после адиабатного расширения. Из последних двух уравнений:  , а следовательно,
, а следовательно,  . После подстановки числовых значений и вычисления:
. После подстановки числовых значений и вычисления:
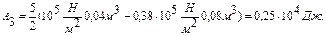
Ответ: 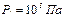 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Дата добавления: 2014-10-31; просмотров: 378; Мы поможем в написании вашей работы!; Нарушение авторских прав |