
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм расчета общего индекса
Общий индекс 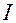 рассчитывается для разнородных единиц совокупности по следующему алгоритму:
рассчитывается для разнородных единиц совокупности по следующему алгоритму:
.
Второй сомножитель - вес. Для количественных показателей весом является цена базисного периода. Для индексов качественных показателей берется количество данного периода 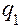 . Такая форма общего индекса называется агрегатной.
. Такая форма общего индекса называется агрегатной.
Общие (агрегатные) индексы следует исчислять по формулам:
а) общий индекс физического объема:
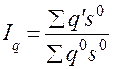 ;
;
б) общий индекс цен:
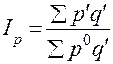 (формула Пааше);
(формула Пааше);
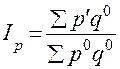 (формула Ласпейреса);
(формула Ласпейреса);
в) общий индекс себестоимости продукции:
 ;
;
г) общий индекс затрат:
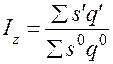 ; где z=sq.
; где z=sq.
д) общий индекс стоимости:
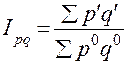 .
.
Следует изучить правила построения индексов. Уяснить правило выбора веса для количественных (объем производства, объем проданной продукции) и качественных (себестоимость, цена) показателей при построении агрегатных индексов. Уяснить правило взаимосвязи индексов: индексы взаимосвязанных величин находятся в той же зависимости, что и сами величины.
Например, 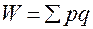 ,
,
где 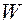 - товарооборот;
- товарооборот; 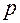 - цена;
- цена;  - объем проданной продукции.
- объем проданной продукции.
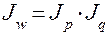 ,
,
отсюда  или
или 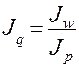 .
.
Часть задач составлена на расчет индекса переменного состава, индекса фиксированного (постоянного) состава и индекса структурных сдвигов.
Индекс переменного состава равен соотношению средних уровней изучаемого признака. Если изучается динамика средней себестоимости одноименной продукции на двух и более предприятиях, то индекс себестоимости переменного состава исчисляется по формуле:
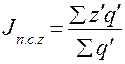 :
: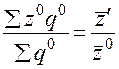 .
.
Изменение средней себестоимости единицы продукции может быть обусловлено изменением себестоимости единицы продукции на каждом предприятии и изменением структуры производства. Индекс переменного состава характеризует влияние изменения обоих факторов на динамику среднего показателя.
Изменение средней себестоимости единицы продукции за счет изменения только себестоимости на каждом предприятии характеризует индекс себестоимости постоянного (фиксированного) состава или индекс себестоимости в постоянной структуре:
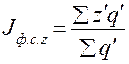 :
: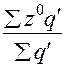 =
= 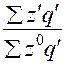
Изменение средней себестоимости единицы продукции только за счет изменения структуры (удельного веса количества произведенной продукции) на отдельных предприятиях изучается при помощи индекса структурных сдвигов:
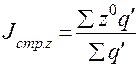 :
: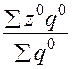 .
.
Индекс структурных сдвигов можно исчислить, используя правило взаимосвязи индексов:
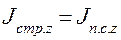 :
: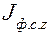 .
.
Часть задач составлена на расчет среднеарифметического или среднегармонического индексов. Их практическое применение зависит от исходной статистической информации.
Если у агрегатного индекса реальная величина в числителе, то преобразуем в среднегармоническую форму; если реальная величина у исходного агрегатного индекса в знаменателе, то преобразуем в среднеарифметическую форму. Например, индекс цен:
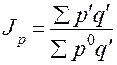 ;
;
Если известен фактический товарооборот отчетного периода – 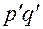 (в числителе), но неизвестна цена базисного года –
(в числителе), но неизвестна цена базисного года – 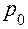 , то заменив
, то заменив 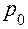 значением из индивидуального индекса цен:
значением из индивидуального индекса цен:
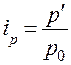 ; (
; ( 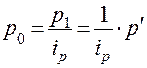 ),
),
получим: 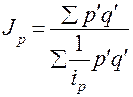 - среднегармонический индекс цен.
- среднегармонический индекс цен.
Агрегатный индекс физического объема может быть преобразован в среднеарифметический индекс, т.е.
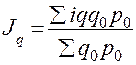 .
.
Пример 1: Имеются данные о продаже акций на фондовом рынке:
| Серия | Дата 12.01. | Дата 17.01. | ||
| Цена, руб. | Объем продаж, шт. | Цена, руб. | Объем продаж, шт. | |
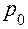
| 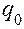
| 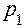
| 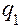
| |
| А Б |
Определите индивидуальные и общие индексы физического объема продаж, цен и товарооборота в фактических ценах (товарооборот в стоимостном выражении).
Решение:
1) По акциям серии А:
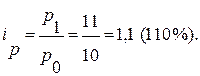
Вывод: Цена акций серии А на торгах 17.01 по сравнению с торгами 12.01 выросла в 1,1 раза (или на 10%).
.
Вывод: Объем продаж акций серии А на торгах 17.01 по сравнению с торгами 12.01 снизился в 0,388 раза (или упал на 61,2%).
2) По акциям серии Б:
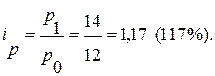
Вывод: Цена акций серии Б на торгах 17.01 по сравнению с торгами 12.01 выросла в 1,17 раза (или на 17%).
.
Вывод: Объем продаж акций серии Б на торгах 17.01 по сравнению с торгами 12.01 снизился в 0,8 раза (или упал на 20%).
3) Общий индекс цен:
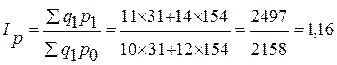
Вывод: Цена продаж на торгах 17.01 по сравнению с торгами 12.01 выросла в 1,16 раза (или на 16%).
4) Объем продаж:
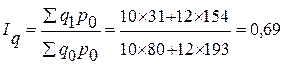
Вывод: Объем продаж на торгах 17.01 по сравнению с торгами 12.01 снизился в среднем в 0,69 раза (или на 31%).
5) Индивидуальный индекс стоимости:
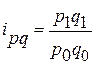
6) Общий индекс стоимости:
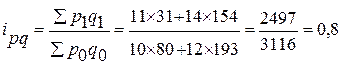
Вывод: Общая стоимость проданных акций снизилась на 20%.
Пример 2: В отчетном месяце по сравнению с предыдущим цены выросли в 1,2 раза, стоимость проданных товаров уменьшилась на 10%. Как изменилось количество проданных товаров?
Решение:
 .
.  .
. 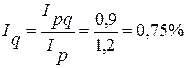 ,
,
т.е. количество проданных товаров снизилось на 25% (100%-75%).
Дата добавления: 2015-01-01; просмотров: 269; Мы поможем в написании вашей работы!; Нарушение авторских прав |