Средняя хронологическая

Средняя хронологическая применяется когда значения признака Х заданы на несколько дат внутри периода. Формула средней хронологической:

,

где, - число дат, на которые известны значения Х.

Пример 1:Остатки денежных средств на расчетном счете предприятия (в т.руб.) характеризуются следующими данными:

Определить: среднедневное наличие денег на расчетном счете за 1-ый квартал, 2-ой квартал и за 1-е полугодие.

За первый квартал:т. руб.

За второй квартал:т. руб.

За полугодие:

т. руб.

Выводы:

1) в первом квартале ежедневно находилось денег на расчетном счете в сумме 206,7тыс. руб.

2) во втором квартале ежедневно находилось денег на расчетном счете в сумме 349,2тыс. руб.

3) в первом полугодии ежедневно находилось денег на расчетном счете в сумме 277,9тыс. руб.

Для изучения внутреннего строения совокупности применяют структурные средние - моду и медиану. По имеющимся данным интервального вариационного ряда нужно исчислить моду, медиану, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.

Мода ( ) - наиболее часто встречающееся значение признака в совокупности. В дискретном ряду мода определяется по наибольшей частоте. Для интервального ряда с равными интервалами мода определяется по формуле:

,

где - нижнее значение модального интервала (имеющего наибольшую частоту);

- ширина (шаг) интервала;

- частота модального интервала;

и - соответственно: частота интервала, предшедствующего (последующего) модальному.

Медиана ( ) - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда:

,

где 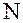– номер медианы.

Для дискретного ряда с четным числом медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда:

.

Для интервального вариационного ряда медиана определяется по формуле:

,

где - нижняя граница медианного интервала;

-его величина; - его частота;

-сумма накопленных частот в интервалах, предшествующих медианному;

-сумма частот ряда.

Не каждая средняя величина является объективной характеристикой изучаемой совокупности. Для расчета типичности средней, колеблемости признака применяются показатели вариации.