Материальный и тепловой балансы реакторов

Исходным уравнением для получения характеристического уравнения реактора любого типа является материальный баланс в следующем виде:

∑m_прих = ∑m_расх.

Составим материальный баланс по исходному веществу А при проведении простой необратимой реакции А → R [6].

В общем виде уравнение материального баланса записывается так

(58)

где – массовый расход

Учитывая, что поступившее в реактор вещество А расходуется в трех направлениях, можно записать

(59)

где – масса вещества А, вступившего в реакционном объеме в химическую реакцию в единицу времени; 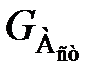– сток вещества А – масса вещества А, выходящего из реакционного объема в единицу времени; – накопление вещества А – масса вещества А, остающегося в реакционном объеме в неизменном виде в единицу времени.

С учетом уравнения (59) уравнение (58) записывается в виде

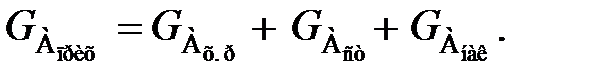(60)

Разность между массой вещества А, поступающего в единицу времени в реактор и выходящего из него – это масса вещества А, переносимого конвективным потоком

(61)

Принимая это во внимание, уравнение (61) можно записать в такой форме

(62)

В каждом конкретном случае уравнение материального баланса принимает различную форму. Оно может составляться для единицы объема реакционной массы, либо для бесконечно малого (элементарного) объема, либо для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем за единицу времени, а можно относить эти потоки к 1 молю одного из исходных реагентов.

Так, в общем случае, когда состав реакционной смеси, температура и другие параметры непостоянны в различных точках реактора или непостоянны во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. В результате получают уравнение конвективного массообмена [10], дополненное членом v_А, который учитывает протекание химической реакции. Составленное по исходному реагенту А, оно имеет вид

(63)

где С_А – концентрация вещества А в реакционной смеси; x, y, z – пространственные координаты; D – коэффициент молекулярной и турбулентной диффузии; v_А – скорость химической реакции.

Член в левой части уравнения (63) отражает общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Этому члену соответствует величина в уравнении баланса (62).

Первая группа членов правой части уравнения (63) – произведения составляющих скорости потока вдоль осей координат на градиенты концентраций – отражает изменение концентрации вещества А в элементарном объеме вследствие переноса его вместе с самой средой в направлении, совпадающем с направлением общего потока.

Вторая группа членов правой части уравнения (63) – произведение D на сумму вторых производных от концентрации по x, y, z – выражает изменение концентрации вещества А в элементарном объеме в результате переноса его путем диффузии. Суммарному переносу вещества в движущейся среде конвективным переносом и диффузией соответствует в уравнении (62) величина (суммарный перенос вещества называют конвективным массообменном, или конвективной диффузией).

Член v_А показывает изменение массы вещества А в элементарном объеме за счет химической реакции. Ему в уравнении (62) соответствует величина .

В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (63) упрощается и решение его значительно облегчается. В том случае, когда параметры процесса постоянны по всему объему реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, взяв разность значений на входе в реактор и выходе из него.

Согласно классификации реакторов, все процессы, протекающие в химических реакторах, делят на стационарные (установившиеся) и нестационарные (неустановившиеся). К первым относят процессы, при которых не происходит изменения во времени параметров процесса (например, концентрации вещества А, температуры и т. д.), поэтому в таких реакторах отсутствует накопление вещества (или тепла) и производная от параметра по времени равна нулю. Так, при стационарном режиме для компонента А

а следовательно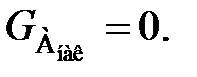

При нестационарных режимах параметры непостоянны во времени, и всегда имеется накопление вещества (тепла), т. е.

поэтому

Как уже отмечалось, уравнение материального баланса является исходным при расчете реактора любого типа. Вместе с тем оно не позволяет учитывать тепловой режим в реакторе и влияние температуры на степень и скорость превращения реагентов.

Поэтому при выборе оптимального режима в реакторе, разработке методов его поддержания, расчета реакторов и теплообменной аппаратуры материальный баланс реактора должен решаться совместно с тепловым балансом.

Исходным уравнением для расчета реакторов с учетом переноса тепла является уравнение теплового баланса, которое обычно составляют по одному из компонентов реакционной смеси [6].

Тепловой баланс в общем виде можно представить уравнением

Q_прих = Q_расх, (64)

где Q_прих – количество тепла, поступающего в реактор в единицу времени; Q_расх – количество тепла, расходуемое в единицу времени.

Рассмотрим случай, когда простая необратимая реакция А → R протекает с выделением тепла, т. е.

А → R + Q,

тогда приход тепла можно записать в виде

Q_прих = Q_{х. р} + Q_реаг, (65)

где Q_{х. р} – количество тепла, выделяющееся в результате химического превращения вещества А в единицу времени; Q_реаг – количество тепла, вносимое исходными реагентами, поступающими в реактор в единицу времени.

Расход тепла может быть представлен уравнением

Q_расх = Q_прод + Q_нак + Q_т, (66)

где Q_прод – количество тепла, уносимое из реактора продуктами реакции в единицу времени; Q_нак – количество тепла, накапливающееся в реакторе в единицу времени; Q_т – количество тепла, расходуемое в единицу времени в результате теплообмена с окружающей средой.

Подставив (65) и (66) в уравнение (64), получим

Q_{х. р} + Q_реаг = Q_прод + Q_нак + Q_т. (67)

После перестановки членов уравнение (67) может быть записано в виде

Q_нак = – (Q_прод– Q_реаг ) – Q_т + Q_{х. р}. (68)

Разность между теплом, уносимым из реактора нагретыми продуктами реакции, и теплом, вносимым в реактор исходными реагентами, представляет конвективный поток тепла

Q_конв = Q_прод – Q_реаг. (69)

С учетом выражения (69) уравнение (68) примет вид

Q_нак = – Q_конв – Q_т + Q_{х. р}. (70)

Уравнение теплового баланса (70) может принимать различную форму в зависимости от типа реактора и теплового режима процесса.

В общем случае имеет место изменение параметров процесса (температуры, концентрации и т. п.) по объему реактора или во времени, в связи с чем тепловой баланс так же, как и материальный, составляют в дифференциальной форме. Для этой цели используют дифференциальное уравнение конвективного теплообмена [10], в которое вводят дополнительные члены, учитывающие отвод тепла в результате теплообмена и тепло реакции. С такими дополнениями уравнение имеет вид

(71)

где ρ – плотность реакционной смеси; С_р – удельная теплоемкость реакционной смеси; х, y, z – пространственные координаты; W_x, W_y, W_z – составляющие скорости движения потока в направлении осей Х, Y, Z; λ – коэффициент молекулярной и турбулентной теплопроводности реакционной смеси; F_уд – удельная поверхность теплообмена; K – коэффициент теплопередачи; ΔТ = Т – Т_т; Т – температура реакционной смеси; Т_т – температура в теплообменнике; v – скорость химической реакции; ΔН – изменение энтальпии реакции.

Группа членов левой части уравнения (71) выражает скорость накопления тепла в элементарном объеме, для которого составляется тепловой баланс. Этому члену соответствует величина Q_нак из уравнения (70), т. е.

Q_нак = . (72)

Первая группа членов правой части уравнения (71) отражает конвективный перенос тепла по соответствующим координатам (х, y, z) в элементарном объеме.

Вторая группа членов правой части уравнения (71) выражает изменение количества тепла, связанное с теплопроводностью (λ) реакционной среды.

Суммарному переносу тепла конвективным потоком, учитывающим влияние теплопроводности, соответствует в уравнении (70) член Q_конв, в результате чего можно записать

Q_конв = . (73)

Из сравнения уравнений (70) и (71) далее следует, что

Q_т = (74)

Q_{х. р} = (75)

Решение уравнения (71) часто связано с большими трудностями. Однако, как будет показано далее, в зависимости от характера протекающей реакции, гидродинамического и теплового режимов в реакторе значение отдельных членов уравнения становится пренебрежимо мало, что приводит к более простым уравнениям, обеспечивающим достаточно точные решения самых разнообразных практических задач.

Уравнения (70) и (71) представляют математическое описание потоков тепла в нестационарном режиме, когда имеет место накопление тепла, и температура процесса изменяется во времени.

Для реакторов непрерывного действия характерен стационарный режим. Неустановившееся состояние наблюдается только в пусковой период и в период остановки реактора. В дальнейшем все реакторы непрерывного действия будут рассматриваться только в стационарном режиме, когда отсутствует накопление тепла, т. е. Q_нак = 0.

В реакторах периодического действия режим всегда нестационарен, происходит накопление тепла в результате химического превращения, и температура в любой точке реактора меняется во времени, т. е. Q_нак ≠ 0. С другой стороны, в реакторах периодического действия отсутствует конвективный перенос тепла, т. е. Q_конв = 0.

Из приведенных примеров следует, что для описания конкретных типов реакторов уравнения (70) и (71) примут более простой вид.