Математические модели процессов в идеальных реакторах

Математическая модель реактора – некоторое упрощенное изображение процесса в реакторе, которое сохраняет наиболее существенные свойства реального объекта и передает их в математической форме [1]. Модели идеальных химических реакторовпредставлены на рис. 14.

Рассмотрим сначала реакторы, работающие в изотермическом режиме. Так как в таких реакторах внутри их объема отсутствует движущая сила теплообмена (∆Т = 0), то из математической модели реактора первоначально можно исключить уравнение теплового баланса. В таком случае математическая модель сводится к уравнению материального баланса, учитывающему химическую реакцию и массообмен. Для дальнейшего упрощения математической модели можно выделить в самостоятельную группу реакторы с идеальной структурой потока – идеального смешения и идеального вытеснения. Допущения об идеальной структуре потока позволяют исключить ряд операторов из общего уравнения материального баланса (63) и тем самым существенно упростить расчеты на основе этого уравнения.

V₀, C₀, T₀

V_р V_р

С(t)

T(t)

V₀, C, T

a б

V₀, C₀, T₀ V_р V₀, C, T

в

Рис. 14. Схемы реакторов:

а – реактор идеального смешения периодический (РИС-П); б – реактор идеального смешения

непрерывный (проточный) (РИС-Н); в – реактор идеального вытеснения (РИВ):

V_р – реакционный объем; С₀, С – концентрация реагента на входе в реактор и выходе из него;

Т₀, Т – температура на входе и выходе

Реакторы периодические характеризуются одновременной загрузкой реагентов. При этом процесс складывается из трех стадий: загрузки сырья, его обработки (химического превращения) и выгрузки продукта. После проведения этих операций они повторяются вновь, т. е. работа реактора осуществляется циклически.

Время одного цикла, проводимого в периодическом реакторе, определяется уравнением

τ_п = τ + τ_в, (76)

где τ_п – полное время цикла; τ – рабочее время, затрачиваемое на проведение химической реакции; τ_в – вспомогательное время, затрачиваемое на загрузку реагентов и выгрузку продукта.

Реактор идеального смешения периодический (РИС-П). Это реактор периодического действия с перемешивающим устройством. Перемешивание в таком реакторе настолько интенсивное, что в каждый данный момент времени концентрация реагентов одинакова по всему объему реактора и меняется лишь во времени по мере протекания химической реакции [10].

Изменение концентрации исходного вещества А во времени и по объему для реакции, протекающей в периодическом реакторе идеального смешения, показано на рис. 15.

Периодические процессы по своей природе всегда являются нестационарными, так как в них за счет химической реакции происходит изменение во времени параметров процесса, например концентрации веществ, участвующих в реакции, т. е. имеет место накопление вещества.

С_А С_Аt = 0

С_А0 С_А0

С_А С_А С_А1 t = t₁

t t

а б

Рис. 15. Распределение концентрации реагента А в РИС-П:

а – по времени; б – по объему: С_А0, С_А1 – концентрация реагента А

в реакционной смеси соответственно в начале и конце процесса; t – время

Математической моделью РИС-П является его характеристическое уравнение. Исходя из этого уравнения, представляется возможным установить размеры реактора, а также исследовать эту модель с точки зрения определения оптимальных значений всех параметров, входящих в характеристическое уравнение.

Исходным соотношением для получения характеристического уравнения реактора, как уже отмечалось, является уравнение материального баланса в дифференциальной форме (63).

В РИС-П все параметры (в том числе и концентрация С_А реагента А) одинаковы по всему объему реактора в любой момент времени, так как реакционная смесь интенсивно перемешивается. Производная любого порядка от концентрации по х, y, z равна нулю, поэтому можно записать

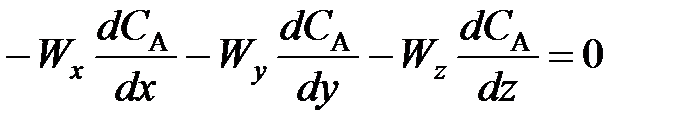; (77)

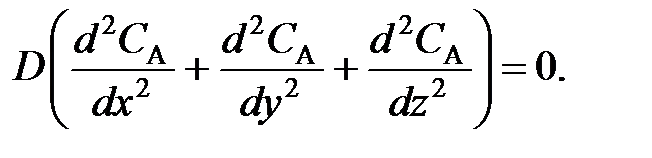(78)

С учетом полученных значений уравнение (63) упрощается и может быть записано не в частных производных, а в виде обыкновенного дифференциального уравнения:

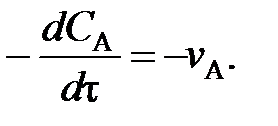(79)

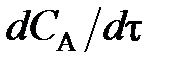При выражении скорости реакции по исходному веществу А . Поэтому перед и v_A ставят знак «–», чтобы скорость являлась положительной величиной.

Текущую концентрацию реагента А рассчитывают по уравнению

(80)

где N_А – начальное химическое количество исходного вещества А в реакционной смеси; V – объем реакционной смеси.

Все реакции протекают либо без изменения, либо с изменением объема реакционной смеси. Для реакций первого типа (V = const) текущая концентрация реагента А составляет

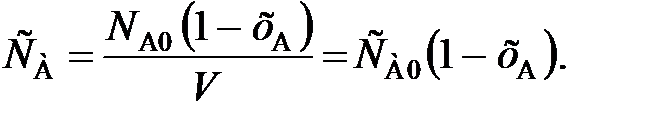(81)

Подставив полученное выражение для С_А в уравнение (79), находим

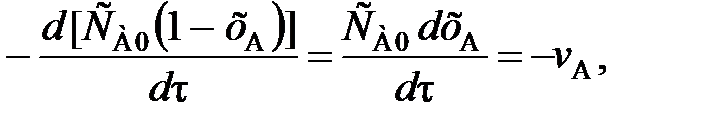(82)

или

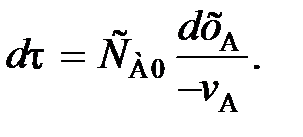(83)

Интегрируя уравнение (83) в пределах изменения времени от 0 до τ и степени превращения от 0 до х_А, получаем характеристическое уравнение РИС-П для условий, когда объем реакционной смеси не изменяется в течение процесса:

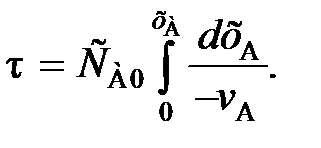(84)

Рассмотрим некоторые частные случаи этого уравнения.

Для необратимой реакции n-го порядка скорость реакции выражается уравнением

–v_A (85)

где k – константа скорости химической реакции.

Подставив полученное значение для –v_A в уравнение (84) и учитывая, что константа скорости k – величина постоянная в изотермических условиях, получим

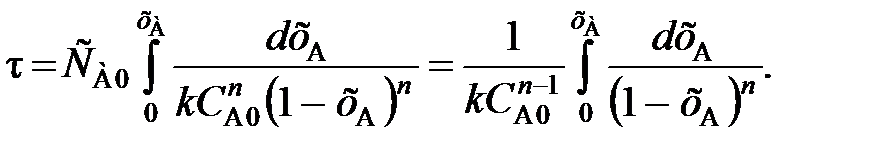(86)

Для необратимой реакции нулевого порядка формула имеет вид

–v_A = k = k. (87)

Поэтому из уравнения (84) следует, что

(88)

Для необратимой реакции первого порядка выражение примет следующий вид:

–v_A = k = k 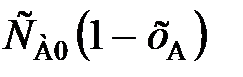, (89)

поэтому подстановкой этого значения в уравнение (84) получаем

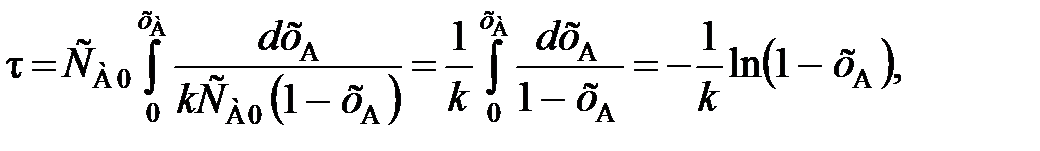(90)

или

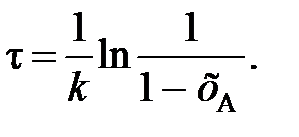(91)

В тех случаях, когда интегрирование уравнения (84) связано с трудностями, определение времени τ производят методом графического интегрирования. Для этого строят графическую зависимость 1 / (– v_А) от х_А и вычисляют площадь под кривой между начальным х_А0 и конечным х_А значениями степени превращения. Для х_А0 = 0 искомая площадь (рис. 16) выражается уравнением

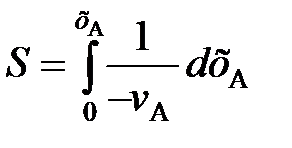. (92)

Подставив полученное значение для S в уравнение (84), находим

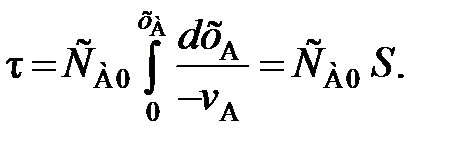(93)

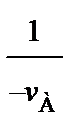
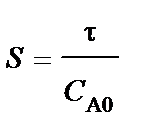
0 х_А х_А

Рис. 16. Графический расчет реактора идеального смешения периодического

Реакторы непрерывного действия (проточные реакторы): реактор идеального смешения (РИС-Н) и реактор идеального вытеснения (РИВ).В реакторах непрерывного действия питание их реагентами и отвод продуктов реакции осуществляется непрерывно.

Если в периодическом реакторе можно непосредственно (по часам) измерить продолжительность реакции, так как показатели процесса меняются во времени, то в реакторе непрерывного действия это сделать невозможно (при установившемся режиме параметры не меняются со временем). Поэтому для непрерывных реакторов удобней пользоваться понятием условного времени пребывания реагентов в системе (времени контакта), которое определяется уравнением

τ = 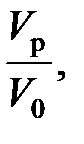(94)

где τ – время пребывания; V_р – объем реактора; V₀ – объем реакционной смеси, поступающей в реактор в единицу времени (объемный расход реагентов), измеренный при определенных условиях.

Поскольку В_А0 = С_А0V₀, где В_А0 – молярный расход реагентов, то выражение (94) может иметь вид

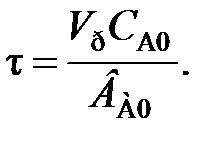(95)

Проточные реакторы отличаются различным характером перемещения в них вещества (гидродинамической обстановкой). По этому признаку непрерывные реакторы разделяют на реакторы идеального вытеснения (РИВ) и реакторы идеального смешения (РИС).

Реактор идеального вытеснения представляет собой трубчатый реактор с отношением длины трубки L к ее диаметру d большим 20, в который подаются исходные реагенты, превращающиеся по мере перемещения их по длине реактора в продукты реакции (рис. 17).

dV

В_А0, С_А0, х_А0 С_А, х_А

L

С_А

С_А0

С_А

х_А L l

х_А0

0 L l

Рис. 17. Изменение концентрации и степени превращения реагента А

по длине реактора (В_А – расход реагента А, кмоль/ч)

Гидродинамический режим в РИВ характеризуется тем, что любая частица потока движется только в направлении основного потока в реакторе, обратное перемешивание отсутствует, как и перенос вещества по сечению, перпендикулярному направлению основного потока (радиальное), так как предполагается, что распределение вещества по этому сечению равномерное.

Каждый элемент объема реакционной массы dV_р движется по длине реактора, не смешиваясь с предыдущими и последующими элементами объема, и ведет себя как поршень в цилиндре, вытесняя все, что находится перед ним. Поэтому этот режим движения реагентов называют также поршневым, или режимом полного вытеснения.

Состав такого элемента объема последовательно изменяется по длине реактора, вследствие протекания химической реакции. Например, концентрация исходного реагента А постепенно изменяется по длине реактора от начального значения С_А0 до конечного С_А (см. рис. 17). Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же.

Для получения характеристического уравнения РИВ исходят из дифференциального уравнения материального баланса (63), упрощая его на основе указанных выше особенностей этого реактора. Поскольку в РИВ реакционная смесь двигается только в одном направлении (по длине l), то для первой группы членов правой части уравнения (63) можно записать (выбрав за направление оси Х направление движения потока реагентов в реакторе):

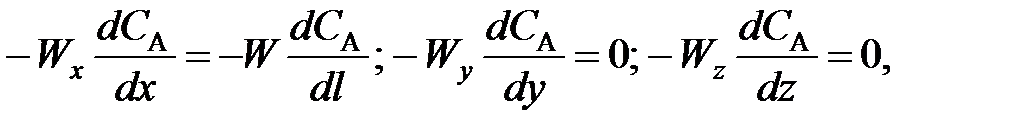(96)

где W – линейная скорость движения реакционной смеси в реакторе; l – длина пути, пройденного элементом объема реакционной смеси в реакторе.

Так как каждый элемент объема реакционной смеси в реакторе не смешивается ни с предыдущим, ни с последующим объемами, а также отсутствует радиальное перемешивание (т. е. нет ни продольной, ни радиальной диффузии), то

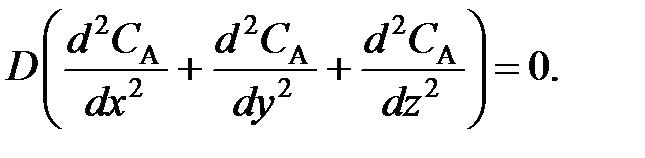(97)

С учетом вышесказанного уравнение (63) для реакторов идеального вытеснения принимает вид

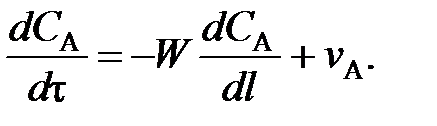(98)

Это уравнение материального баланса является математическим описанием потоков реагентов в РИВ при нестационарном режиме (таком, когда параметры процесса меняются не только по длине реактора, но и непостоянны во времени). Такой режим характерен для периодов пуска и остановки реактора. Член dC_A / dτ характеризует изменение концентрации вещества А во времени для данной точки реактора – это накопление вещества А в этой точке. Из уравнения (98) видно, что накопление зависит от конвективного переноса вещества в данной точке реактора 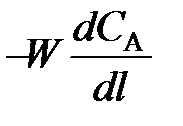и от расхода вещества на химическую реакцию v_А.

Стационарный режим характеризуется тем, что параметры в данной точке реакционного объема не меняются во времени, т. е. dC_A / dτ = 0. Тогда уравнение (98) примет вид

(99)

Уравнение (99) показывает, что при стационарном режиме изменение в потоке массы вещества А в данной точке реактора равно скорости расходования вещества А на химическую реакцию.

Из уравнения (99) легко получить характеристическое уравнение РИВ. Если объем реакционной смеси не изменяется в процессе, то справедливо уравнение (81), после дифференцирования которого получим

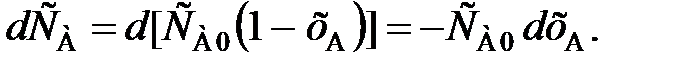(100)

Длину пути l можно выразить как произведение (W τ), откуда при постоянной линейной скорости потока

dl = W dτ. (101)

Подставив (100) и (101) в уравнение (99), находим

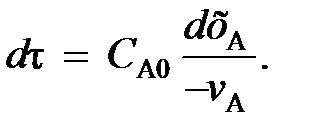(102)

После интегрирования уравнения (102) в пределах изменения степени превращения от 0 до х_А получаем характеристическое уравнение РИВ

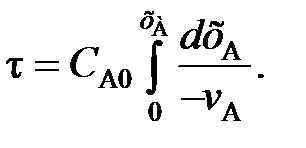(103)

Уравнение (103) для РИВ аналогично уравнению (84), полученному для РИС-П. В уравнении (84) время τ есть время проведения реакции в периодическом реакторе (от загрузки сырья до выгрузки продуктов), а в уравнении (103) τ – время, в течение которого реакционная смесь проходит через РИВ от входа в реактор до выхода из него (при условии, что реакция идет без изменения объема).

Уравнение (103) для необратимой реакции n-го порядка примет вид

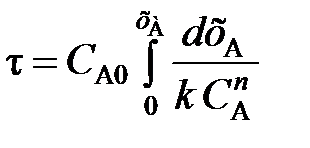(104)

или с учетом уравнения (81)

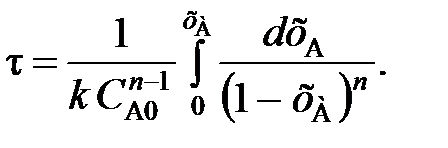(105)

Для реакции нулевого порядка формула имеет вид

(106)

Для необратимой реакции первого порядка можно записать, что

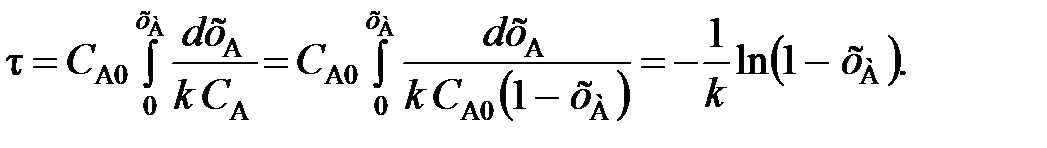(107)

Для реакций более высоких порядков целесообразно для определения времени пребывания использовать метод графического интегрирования. Для этого строят графическую зависимость 1 / (– v_А ) от х_А (рис. 18) и вычисляют площадь под кривой S_выт между начальным и конечным значениями степени превращения х_А0 и х_А:

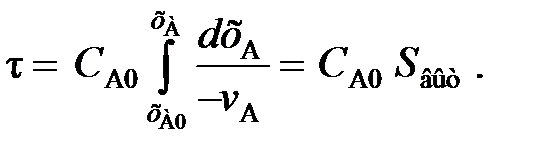(108)

До сих пор речь шла о реакциях, идущих без изменения объема. Если же в ходе реакции объем изменяется, то необходимо учитывать, что концентрация вещества А изменяется не только за счет химического превращения, но и за счет изменения объема реакционной смеси, поэтому текущая концентрация вещества А не может быть рассчитана по уравнению (83).

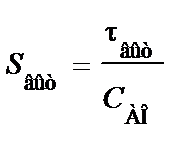
0 х_А0 х_А х_А

Рис. 18. Графический расчет реактора идеального вытеснения

Изменение объема реакционной смеси учитывают с помощью коэффициента относительного изменения объема

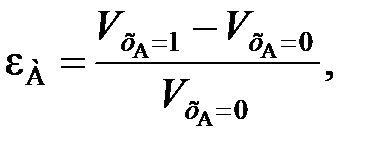(109)

где ε_А – коэффициент относительного изменения объема реакционной смеси при изменении х_А от 0 до 1; 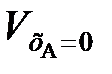, 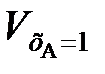– объемы реакционной смеси соответственно при х_А = 0 и х_А = 1.

В частном случае, при линейном изменении объема реакционной смеси V от степени превращения, можно записать

V = V₀ (1 + ε_А х_А), (110)

где V₀ – первоначальный объем смеси.

При подстановке значения V из уравнения (110) в уравнение (80) получаем уравнение для расчета текущей концентрации С_А при степени превращения х_А с учетом изменения объема реакционной смеси:

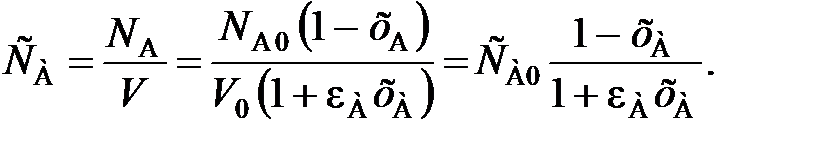(111)

Изменение объема реакционной смеси в зависимости от степени превращения х_А учитывают и при выводе характеристических уравнений реакторов. Так, например, характеристическое уравнение реактора идеального вытеснения (103) с учетом уравнения (111) записывается для реакции n-го порядка в виде

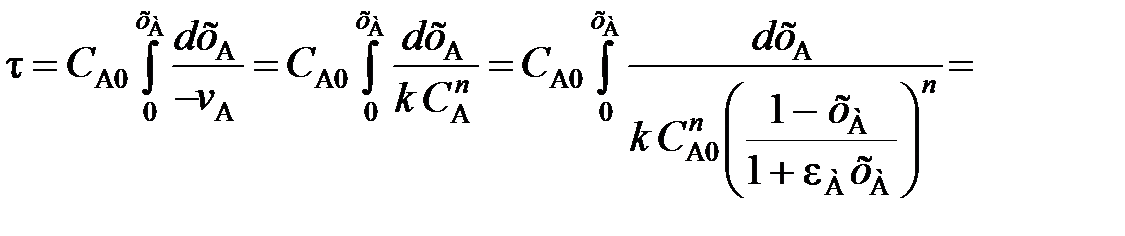
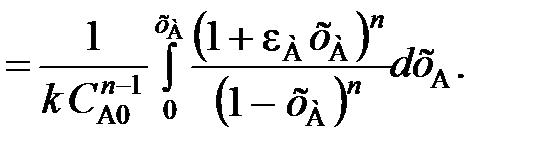(112)

Непрерывный реактор идеального смешения (РИС-Н) – это реактор с мешалкой, в который непрерывно подают реагенты и выводят из него продукты реакции. Благодаря интенсивному перемешиванию потоков мгновенно устанавливается одинаковая по всему объему реактора концентрация реагента А, равная его концентрации на выходе из реактора. Резкое изменение концентрации при входе реагентов в реактор происходит за счет мгновенного смешения поступающих реагентов с реакционной массой, уже находящейся в реакторе, где концентрация компонента А значительно ниже, чем в подаваемой реакционной смеси.

Величина перепада между начальной С_А0 и конечной С_А концентрациями исходного реагента зависит при прочих равных условиях от величины скорости химической реакции. Чем она выше, тем меньше концентрация реагента А в реакторе и больше перепад (С_А0 – С_А). С другой стороны, при одной и той же скорости реакции величина перепада зависит от времени пребывания (τ) реагентов в реакторе. Чем выше τ, тем полнее проходит реакция и тем ниже концентрация реагента С_А в реакционной смеси (рис. 19). Точка, соответствующая входу реагентов в реактор, нанесена на оси абсцисс правее начала координат, что дает более наглядное представление об изменении концентрации при входе реакционной смеси в реактор.

С_А

С_А0

С_А1 t₁

С_А2 t₂

С_А3 t₃

Y₀ Y

Рис. 19. Концентрация реагента А в РИС-Н

при различном времени пребывания реагентов в реакторе (t_{1 <} t_{2 <} t₃):

Y – координата объема; Y₀ – координата, характеризующая вход реагентов в реактор

Так как концентрация реагентов в проточном реакторе идеального смешения одинакова во всех точках реакционного объема, то постоянны по объему и другие параметры – степень превращения и скорость реакции (рис. 20).

Материальный баланс по какому-либо компоненту, необходимый для получения характеристического уравнения, составляют с использованием концентраций реагента на входе в реактор и выходе из него, т. е. применяя уравнение (62). При стационарном режиме = 0, поэтому

(113)

где В_А – молярный расход; G_А – массовый расход.

х_А

х_{А к}

х_А0

Y₀ Y

а

–v_A

–v_A0

–v_Aк

Y₀ Y

б

Рис. 20. Изменение параметров в РИС-Н:

а – степени превращения х_А; б – скорость процесса v_А

Из уравнения (113) видно, что условием стационарности процесса является равенство скорости конвективного переноса вещества А и скорости его химического превращения. Найдем значения величин, входящих в уравнение (113). По уравнению (61)

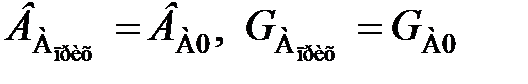; (114)

; (115)

, (116)

где V_р – объем реактора.

Подставляя (114)–(116) в (113), получаем

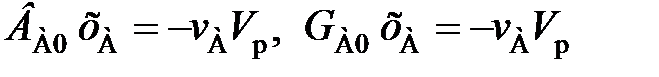(117)

или, учитывая, что , где V – объемный расход реагентов, имеем

(118)

Отношение V_p / V – это условное время пребывания τ (см. (88)). Тогда

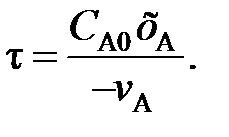(119)

Это характеристическое уравнение реактора идеального смешения. Для более общего случая, когда начальная степень превращения х_А0 не равна нулю, оно записывается

(120)

Для простой необратимой реакции n-го порядка с учетом уравнения (81) уравнение (119) примет вид

. (121)

Для реакции нулевого порядка можно записать, что

(122)

Для реакции первого порядка формула примет вид

(123)