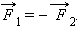Второй закон Ньютона, масса и вес тела

Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований, Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение. Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу. Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = a*t²/2 определим ускорение а.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку a₁/a₂= F₁/F₂

a F Отношение силы, действующей на тело, к ускорению есть величена постоянная, которую обозначим т. Это отношение назовем массой тела.

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку). Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть 1 или а т Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела. Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так: где а — ускорение, т — масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила. Результирующая сила F равна векторной сумме всех сил, приложенных к телу; тогда уравнение согласно второму закону Ньютона запишется так: п где знак «сигма» 2 означает сумму, то есть F — та. Следовательно, сила равна произведению массы на ускорение. Второй закон динамики можно записать в иной более удобной форме. Уч-итывая, что ускорение подставим это выражение в уравнение второго закона Ньютона. Получим „ /ш> а — mi»! Л (то) Г — та = ----:—-—:----- = -----д7---- Импульсом, или количеством движения, называется вектор, ный произведению массы тела на его скорость (mv). Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени Р__ . Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данном теле. Это определение несовершенно. Из второго закона Ньютона вытекает следующее определение массы. Из равенства— = — видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот. Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности.'Тогда можно сказать, что масса есть мера инертности тела. Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону: m =------r m" . •, (3) где m — масса тела, движущегося со скоростью v; m0 — масса этого же тела, находящегося в покое; с = 3 • 1 08 -^-— скорость света в вакууме. Проанализируем данное уравнение: 1) если у <^ с, то величиной — j- , как очень малой, можно пренебречь и m = m0, .то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения; 2) если v » с, to—fszl, тогда т=— -; отсюда вытекает, что' с, to—fszl, тогда т=— - т -> оо. По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы. Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует. Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно. Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях. Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества. Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю. Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже). Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при v0 = 0) называется свободным падением. Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р. Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес. Если Р — сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаково и среднее его значение равно 9,8 м/с2), то применяя второй закон динамики, получим Р = mg. Выразим с помощью этой формулы веса двух различных тел. Тогда: PI = mig и />2 = mzg. Разделив почленно эти два равенства, будем иметь Л щ i Рг т2 Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

7.2

Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля и и утри замкнутого проводящего контура в нем возникнет электрический ток, который называют индукционным током. Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 23). Если радом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 24). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное иоле всегда порождает переменное электрическое поле.

Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина — магнитный поток. Магнитным потокомчерез замкнутый контур площадью (рис. 25) называют физическую величину, равную произведению модуля вектора магнитной индукции 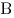на площадь контура и на косинус угла между направлением вектора магнитной индукции и нормалью к площади контура: .

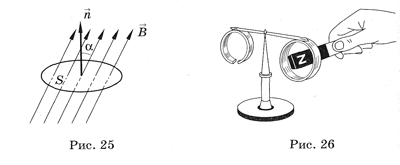
Опытным путем был установлен основной закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через контур: . Если рассматривать катушку, содержащую n витков, то формула основного закона электромагнитной индукции будет выглядеть так: .

Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 В • с.

Из основного закона следует смысл размерности: 1 вебер — это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.

Классической демонстрацией основного закона электромагнитной индукции является опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур. В соответствии с правилом Ленца в законе электромагнитной идукции цолжен стоять знак минус:

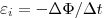
Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло (рис. 26). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.

7.1

В §1.7 понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений

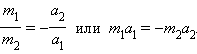
В векторной форме это соотношение принимает вид

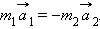
Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силам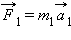и и возникающими при взаимодействии тел. Отсюда следует:

Это равенство называется третьим законом Ньютона.