
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Количественная оценка корреляционных взаимосвязей признаков
На основе примера, представленного в таблице 1.1, рассмотрим последовательность и экономическую интерпретацию различных статистических методов, позволяющих подтвердить или опровергнуть наличие зависимости между размером инвестиций, направленных в основной капитал, и налоговыми платежами малых предприятий с учетом временного лага.
Таблица 1.1
Исходная статистическая информация по реализации инвестиционной программы
| № п/п | Размер инвестиций в основной капитал в период их освоения, тыс. руб. | Налоговые платежи в отчетном периоде, тыс. руб. | № п/п | Размер инвестиций в основной капитал в период их освоения, тыс. руб. | Налоговые платежи в отчетном периоде, тыс. руб. |
| Усл. обозн. | Услов. обозн. | ||||
| 13. | |||||
| 14. | |||||
| 15. | |||||
| 16. | |||||
| Итого | |||||
| В среднем | 600,0 | 507,9 |
1. Выбор статистических методов исследования определяется типом связи между изучаемыми явлениями, которые в статистике классифицируются как функциональные и статистические. Разновидностью последних при оценке большинства взаимосвязей, возникающих в экономике, выступают корреляционные связи. В нашем случае корреляционная связь характеризуется тем, что разным значениям размера выделенных инвестиций отдельным хозяйствующим субъектам соответствует множество изменяющихся значений налоговых платежей, т. е. налоговые платежи в каждом конкретном случае обладают большой вариацией. Отсюда существующая, или не существующая при этом закономерность в изменениях результативного признака от размера выделенных инвестиций проявляется только в его средних значениях.
При выборе факторов, определяющих количественные взаимосвязи между признаками довольно часто необходимо учитывать временной лаг, характеризующийся тем, что одно из выбранных для анализа явлений по сравнению с другим, связанным с ним имеет отставание во времени. Так инвестиции в основной капитал дадут отдачу не в год их освоения, а позже. По этой причине размер налоговых платежей в рассматриваемом случае относится к отчетному периоду.
Приступая к количественной оценке корреляционных взаимосвязей признаков необходимо:
· выделить факторный признак или признак причины, который обозначается в статистике -  и результативный признак -
и результативный признак -  . По данным таблицы 1.1 факторный признак – инвестиции в основной капитал, результативный – размер налоговых платежей;
. По данным таблицы 1.1 факторный признак – инвестиции в основной капитал, результативный – размер налоговых платежей;
· иметь в виду, что объем совокупности, по которой рассчитываются количественные характеристики, должен как минимум в 5-6 и более раз превышать число факторов, участвующих в расчетах;
· обязательное обеспечение качественной однородности изучаемой совокупности. Качественная однородность исследуемой совокупности характеризуется размахом вариации факторного признака, причем в качественно однородной совокупности размах вариации не должен превышать своего трехкратного минимального значения, т. е.
 =
=
2. По результатам статистического наблюдения, представленным в таблице 1.1, зачастую невозможно с уверенностью констатировать, о наличии связи между изучаемыми явлениями. В таких случаях по результатам наблюдения необходимо построить аналитическую группировку, характеризующую зависимость между размером инвестиций в основной капитал и налоговыми платежами. Подлежащее аналитической группировки строится по факторному признаку. При построении аналитической группировки необходимо определить:
· число групп в группировке. Для этого используют формулу Стерджесса:

· величину интервала.

При необходимости эта величина округляется, но всегда в сторону увеличения.
Таблица 1.2
Построение промежуточной таблицы
| Группы предприятий по размеру выделенных инвестиций в основной капитал, тыс. руб. | Номер предприятия | Сумма инвестиций по группе предприятий, тыс. руб. | Сумма налоговых платежей по группе предприятий, тыс. руб. |
| Первая группа 300-420 | 3; 9. | 300+330 | 320+369 |
| Итого | ? | ||
| Вторая группа 420-540 | 2; 5; 8. | 500+450+500 | 453+390+370 |
| Итого | |||
| Третья группа 540-660 | 1; 6; 10; 11; 12; 15; 17;19. | 600+550+550+650+570+ +600+600+620 | ? |
| Итого | |||
| Четвертая группа 660-780 | 7; 13; 14; 16. | 760+670+740+750 | 609+591+538+633 |
| Итого | |||
| Пятая группа 780-900 или | 4; 18. | 800+860 | 705+718 |
| Итого | |||
| Всего | ? | ? |
Таблица 1.3
Влияние инвестиций, вложенных в основной капитал на размер налоговых платежей
| Группы предприятий по размеру инвестиций в основной капитал, тыс. руб. | Число предприятий | Средний размер инвестиций по группе предприятий, тыс. руб. | Сумма налоговых платежей по группе предприятий, тыс. руб. | Налоговые платежи | |
| в расчете на одно предприятие, тыс. руб. | в % к предыдущей группе | ||||
| А | |||||
| 300-420 | 315,0= | ? | - | ||
| 420-540 | 483,3 | 404,3 | 117,7 | ||
| 540-660 | 592,5 | 494,2 | 122,2 | ||
| 660-780 | 730,0 | 592,7 | 119,9 | ||
| Более 780 | 830,0 | 711,5 | 120,0 | ||
| Итого | 600,0= | 507,9 | - |
3. Связь между признаками есть – и эта связь корреляционная.
Связь между признаками устойчивая, а увеличение налоговых платежей происходит примерно с одинаковым ускорением. Вывод делается по данным графы 5 таблицы 1.3. Это свидетельствует о том, что корреляционная связь может выражаться линейной связью, а уравнение парной линейной корреляционной связи или линейной регрессии имеет вид:

где  средне значение налоговых платежей при изменении инвестиций в основной капитал;
средне значение налоговых платежей при изменении инвестиций в основной капитал;
 свободный член уравнения парной регрессии;
свободный член уравнения парной регрессии;
 коэффициент регрессии, характеризующий среднее отклонение результативного признака от своей средней величины с изменением признака фактора x на единицу своего измерения, в нашем случае на одну тыс. руб.
коэффициент регрессии, характеризующий среднее отклонение результативного признака от своей средней величины с изменением признака фактора x на единицу своего измерения, в нашем случае на одну тыс. руб.
Определение неизвестных параметров «  » и «
» и «  » линейной корреляционной связи – одна из задач корреляционного анализа. Поставленная задача решается способом наименьших квадратов. В основу этого способа положена теорема, согласно которой сумма квадратов отклонений вариант от средней арифметической величины есть величина минимальная. Количественные значения неизвестных параметров рассчитываются по системе нормальных уравнений для прямой линии. Система нормальных уравнений имеет вид:
» линейной корреляционной связи – одна из задач корреляционного анализа. Поставленная задача решается способом наименьших квадратов. В основу этого способа положена теорема, согласно которой сумма квадратов отклонений вариант от средней арифметической величины есть величина минимальная. Количественные значения неизвестных параметров рассчитываются по системе нормальных уравнений для прямой линии. Система нормальных уравнений имеет вид:
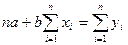

 .
.
Если первое нормальное уравнение разделить на «  », т. е. объем исследуемой совокупности, то получим:
», т. е. объем исследуемой совокупности, то получим:

 , отсюда
, отсюда  .
.
На основе последнего аналитического выражения практические работники, как правило, рассчитывают свободный член уравнения регрессии «  ».
».
Решая систему нормальных уравнений относительно параметра  - коэффициента регрессии, искомая характеристика может быть рассчитана несколькими вариантами в виде:
- коэффициента регрессии, искомая характеристика может быть рассчитана несколькими вариантами в виде:
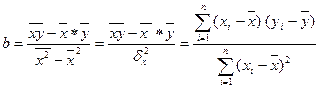 .
.
Использование различных вариантов расчета коэффициента регрессии связано с наличием у пользователя исходной информации. Если расчет параметров уравнения регрессии ведется по первичным данным, т. е. данным, представленным в таблице 1.1, то для интерпретации результатов расчета и использования их в управлении больше подойдет вариант расчета, основанный на отклонениях факторного и результативного признаков от своих средних значений. Предпочтение основывается еще и на том, что параметры корреляции зависят не от уровней признаков, а только от их отклонений от средних значений. Результаты расчета представлены в таблице 1.4.
Для расчета коэффициента регрессии необходимо знать:
· средний размер инвестиций в расчете на одно предприятие: 
· средний размер налоговых платежей: 
Если значения итоговой строки таблицы 1.4 использовать для расчета коэффициента регрессии по аналитическому выражению, представленному ниже, получим:

Рассчитанный коэффициент регрессии решает первую задачу корреляционного анализа – дает количественную оценку влияния размера выделенных инвестиций на поступление налоговых платежей, которую следует интерпретировать так. С увеличением размера инвестиций в основной капитал на 1 тыс. руб., т. е. на единицу своего измерения по сравнению со средней величиной, в среднем по 19 предприятиям, включенным в программу, налоговые поступления увеличивались на 0,69 тыс. руб.
Следующим шагом является расчет неизвестного параметра уравнения регрессии.
 .
.
Уравнение регрессии после нахождения неизвестных параметров имеет вид:

Выполненные расчеты следует интерпретировать так:
· интерпретацию коэффициента регрессии «в» - смотри выше;
·  свободный член уравнения регрессии. Этот показатель может принимать как положительные, так и отрицательные значения. В нашем случае, являясь положительной величиной «
свободный член уравнения регрессии. Этот показатель может принимать как положительные, так и отрицательные значения. В нашем случае, являясь положительной величиной «  » указывает на среднее значение налоговых платежей при отсутствии инвестиций в основной капитал. Этот вывод делается исходя из того, что:
» указывает на среднее значение налоговых платежей при отсутствии инвестиций в основной капитал. Этот вывод делается исходя из того, что:

 , отсюда
, отсюда  .
.
Другими словами  - средний размер поступлений налоговых платежей сформировался под влиянием как инвестиций в основной капитал, так и других признаков, не включенных в расчет.
- средний размер поступлений налоговых платежей сформировался под влиянием как инвестиций в основной капитал, так и других признаков, не включенных в расчет.  - налоговые платежи, сформированные только под влиянием инвестиций в основной капитал.
- налоговые платежи, сформированные только под влиянием инвестиций в основной капитал.
Следует обращать внимание и на такой момент: если «  » - больше нуля, то это указывает на то, что относительное изменение налоговых платежей идет медленнее, чем изменение факторного признака. Если же «
» - больше нуля, то это указывает на то, что относительное изменение налоговых платежей идет медленнее, чем изменение факторного признака. Если же «  » принимает отрицательное значение, то можно интерпретировать только знак этого параметра уравнения регрессии с указанием на то, что изменение результативного признака опережает вариацию факторного признака, т. е.
» принимает отрицательное значение, то можно интерпретировать только знак этого параметра уравнения регрессии с указанием на то, что изменение результативного признака опережает вариацию факторного признака, т. е.
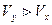 .
.
· фактические налоговые платежи полезно сравнивать с их расчетными значениями. Расчетные или теоретические значения платежей указывают на то, какими были бы налоговые поступления по отдельным организациям, включенным в инвестиционную программу при фактически вложенных в основной капитал размером инвестиций, и средней по совокупности эффективности их использования, измеряемой коэффициентом регрессии. В нашем случае:

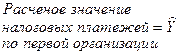 = 93,9+ 0,69 х 600 = 507,9 тыс. руб.
= 93,9+ 0,69 х 600 = 507,9 тыс. руб.
Полученный результат сравнивают с фактическими налоговыми платежами. Так: 8, 10, 11, 14 и др. предприятия явно допустили более низкую по сравнению со средним уровнем по совокупности, эффективность использования вложенных в основной капитал инвестиций;
В практической деятельности на поступление налоговых платежей влияет не только инвестиционная деятельность, но и другие признаки, не включенные в расчет. Такими причинами могут быть:
· кризисные в экономике явления, вызывающие падение спроса на продукцию предприятия;
· снижение платежеспособности покупателей продукции;
· несовершенное законодательство в части покупателей и заказчиков и др.
Очевидно, что неучтенные в расчете факторы могут оказывать отрицательное воздействие на налоговые платежи.
Таблица 1.4
Корреляция между размером инвестиций в основной капитал и налоговыми платежами
| № п/п | Размер инвестиций в основной капитал в период их освоения, тыс. руб., 
| Налоговые платежи в отчетном периоде,
тыс. руб., 
| 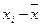
| 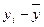
| ( 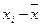 ) ) 
 ( ( 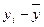 ) )
| ( 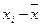 ) ) 
| ( 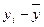 ) ) 
| Расчетные значения налоговых платежей, тыс. руб.,

|
| -12,9 | - | - | 166,41 | 507,9 | ||||
| -100 | -54,9 | +5490 | 10 000 | 3 014,01 | 439,9 | |||
| -300 | -187,9 | +56 370 | 90 000 | 35 306,41 | 300,9 | |||
| +200 | +197,1 | +39 420 | 40 000 | 38 848,41 | 645,9 | |||
| -150 | -117,9 | +17 685 | 22 500 | 13 900,41 | 404,4 | |||
| -50 | -52,9 | +2 645 | 2 500 | 2 798,41 | 473,4 | |||
| +160 | +101,1 | +16 176 | 25 600 | 10 221,21 | 618,3 | |||
| ? | ? | |||||||
| -270 | -138,9 | +37 503 | 72 900 | 19 293,21 | 321,6 | |||
| -50 | -120,9 | +6 045 | 2 500 | 14 616,81 | 473,4 | |||
| +50 | -84,9 | -4 245 | 2 500 | 7 208,00 | 542,4 | |||
| -30 | +98,1 | -2 943 | 9 623,6 | 487,2 | ||||
| +70 | +83,1 | +5 817 | 4 900 | 6 905,61 | 556,2 | |||
| +140 | +30,1 | +4 214 | 19 600 | 906,01 | 604,5 | |||
| -7,9 | - | - | 62,41 | 507,9 | ||||
| ? | ? | |||||||
| +54,1 | - | - | 2 926,81 | 507,9 | ||||
| +260 | +210,1 | +54 626 | 67 600 | 44 142,00 | 687,3 | |||
| ? | ? | |||||||
| Итого | 11 400 | 9 650 | +271 722 | 394 400 | 244 937,4 | 9 650,1 |
Исходя из этого, второй задачей корреляционного анализа является измерение тесноты зависимости между изучаемыми признаками. Для этого рассчитывают:
 =
=  =
= 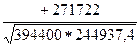 = +0,874
= +0,874
Коэффициент корреляции аналитики называют стандартизированным коэффициентом регрессии. Стандартизированный – указывает на то, что коэффициент корреляции не имеет единиц измерения и показывает как факторный признак, изменяясь на свое среднее квадратическое отклонение, вызывает 0,874 части (доли) среднего квадратического отклонения результативного признака по налоговым платежам.
В управлении для оценки тесноты связи между изучаемыми явлениями удобнее пользоваться коэффициентом детерминации, рассчитанным на основе коэффициента корреляции.
Коэф. детерминации = r2 = (+0?874)2 = 0,7638, т. е. 76,38 % вариации налоговых платежей связано с инвестициями в основной капитал, а 23,62 % налоговых платежей связано с признаками, не включенными в расчет (100 % - 76,38 %).
Если задаться вопросом оценки дальнейшей государственной поддержки организаций исследуемой отрасли, то необходимо измерить надежность рассчитанных коэффициентов корреляции и регрессии. При решении этих вопросов, по мнению ведущих российских статистиков, М. М. Юзбашева и И. И. Елисеевой, необходимо исходить из следующего:
· показатели корреляционной связи, исчисленные по выборочной совокупности, являются оценками закономерности лишь по конкретной совокупности. Поэтому при перенесении выявленных закономерностей на другую совокупность, должно сопровождаться оценкой степени надежности параметров корреляции. Под надежностью в данном случае понимается вероятность того, что значение проверяемого параметра не равно нулю, т. е. не включает в себя величины противоположного знака;
· вероятностная оценка параметров корреляции проводится по общим правилам проверки статистических гипотез, разработанным математической статистикой, путем сравнения оцениваемой величины со средней случайной ошибкой оценки.
Всем явлениям природы и общества присуща вариация, которая может носить как разрушительный характер, так и созидательный. Для статистического изучения вариации строят вариационные ряды, имеющие следующие формы:
· ранжированные. Особенностью этих рядов является то, что перечень отдельных единиц совокупности располагается в порядке возрастания или убывания изучаемого признака;
· дискретные вариационные ряды;
· интервальные вариационные ряды.
Вариационные ряды часто называют рядами распределения. Интервальный вариационный ряд – это структурная группировка. Первые две графы аналитической группировки нашего исследования представим в виде структурной группировки и проведем на основе статистических показателей оценку этого ряда распределения.
Таблица 1.5
Расчет параметров ряда распределения
| Группы предприятий по размеру инвестиций в основной капитал, тыс. руб. | Число предприятий | Середина интервала, тыс. руб. | Накопленная частота | Расчет вариации | |
| 300 – 420 | |||||
| 420 – 540 | |||||
| 540 – 660 | |||||
| 660 – 780 | |||||
| Более 780 | |||||
| Итого | ? |

Тема 2. Динамические ряды и их характеристики
Таблица 2.6
Динамика выручки
| Месяцы | Уровни, тыс. руб. | Абсолютные показатели | Относительные показатели | Знач. 1 % при- роста, тыс.. руб. | |||||
| абсолютное изменение, тыс. руб. | ускорение цепного абсолютного изменения тыс. руб. | темп изменения или темп роста, % | темп прироста, % | ||||||
| базисное | цепное | базисный | цепной | базисный | цепной | ||||
Тема 3. Статистика валового внутреннего продукта
Построение динамических рядов сопоставимых уровней
Таблица 2.7
?
| Годы | ВВП в текущих ценах, млрд. руб. | Индекс-дефлятор ВВП | ВВП в ценах 2000 года, млрд. руб. | |
| по данным Росстата, цепной | базисный | |||
| 7 305,64 | - | 1,0 | 7 305,64 | |
| 8 943,58 | 1,165 | 1,165 | 8 943,58 : 1,165 = 7 676,89 | |
| 10 830,53 | 1,156 | 10 830,53 : 1,346 = 8 046,45 | ||
| 13 243,24 | 1,138 | |||
| 17 048,12 | 1,203 | |||
| 21 625,37 | 1,193 | |||
| 26 917,20 | 1,152 | |||
| 33 247,50 | 1,138 | |||
| 41 276,80 | 1,180 | |||
| 38 786,40 | 1,019 | |||
| 44 939,10 | 1,114 |
Тема 4. Статистика финансов организации
Таблица 3.7
Динамика имущества организации
| Наименование активов | На начало года | На конец года | Структура, % | Абсолютная разность, тыс. руб. | Абсолютная разность в процентах к итогу актива баланса на начало года | |
| на начало года | на конец года | |||||
| Внеоборотные активы | 89,1 | 80,5 | +41010= | + 1,25= | ||
| Оборотные активы всего | 10,9 | 19,49 | +361847 | + 11,04 | ||
| в том числе запасы | 1,4 | |||||
| вся дебиторская задолженность | 3820+282374=286194 | 8312+512876=521188 | + 234994 | +7,17 | ||
| краткосрочные финансовые вложения | ||||||
| денежные средства | ||||||
| Баланс | +402857 | + 12,29= |
Определите:
· как изменился итог баланса организации, и какова скорость его изменения;
· структуру актива баланса и проведите анализ динамики этого показателя;
· влияние изменения каждой статьи баланса на общий итог изменения баланса;
· как изменился пассив баланса за исследуемый период. По проведенному исследованию сформулируйте выводы
Расчеты могут быть дополнены детальным анализом основных средств организации с точки зрения их состояния, движения, использования. Полезно измерить и динамику незавершенного строительства, направленного на инвестиции в основной капитал.
Таблица 3.8
Динамика источников имущества организации
| Источники имущества | На начало года | На конец года | Структура, % | Абсолютная разность, тыс. руб. | Абсолютная разность в процентах к итогу пассива баланса на начало года | |
| на начало года | на конец года | |||||
| Собственный капитал | 90,6 | 80,8 | +5314 | +0,16 | ||
| Долгосрочные обязательства | 0,1 | 0,1 | +2836 | +0,09 | ||
| Краткосрочные обязательства | 9,2 | 18,9 | +394707 | +12,04 | ||
| из них кредиторская задолженность | 8,8 | 18,3 | +384797 | +11,7 | ||
| Баланс | +402857 | + 12,29 |
Вывод.
Рациональная структура баланса на конец года характеризуется так:
Дата добавления: 2015-01-01; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |