СИНУСОИДАЛЬНЫХ СИГНАЛАХ

1. Анциферова И.В. Бухгалтерский финансовый учет: Учебник / И.В. Анциферова. - М.: Дашков и К, 2011. - 556 с.

2. Бабаев Ю.А. Бухгалтерский финансовый учет: Учебник / Ю.А. Бабаев, А.М. Петров, Л.Г. Макарова; Под ред. Ю.А. Бабаева. - 4-e изд., перераб. и доп. - М.: Вузовский учебник: ИНФРА-М, 2011. - 576 с.

3. Бабаев Ю.А. Бухгалтерский финансовый учет.: Учебник для вузов / Ю.А. Бабаев, А.М. Петров, Л.Г. Макарова; Под ред. Ю.А. Бабаева. - 3-e изд., перераб. и доп. - М.: Вузовский учебник: ИНФРА-М, 2010. - 587 с.

4. Бахтурина Ю.И. Бухгалтерский финансовый учет: Учебник / Ю.И. Бахтурина, Т.В. Дедова, Н.Л. Денисов; Под ред. Н.Г. Сапожниковой - М.: ИНФРА-М, 2011. - 505 с.

5. Бровкина Н.Д. Контроль и ревизия: Учебное пособие / Н.Д. Бровкина; Под ред. М.В. Мельника. - М.: ИНФРА-М, 2012. - 346 с.

6. Верховцев А. В. Делопроизводство в бухгалтерии. - 4-е изд., испр. и доп. - (Библиотека журнала "Досье бухгалтера")/Верховцев А. В. ИНФРА-М, 2001. - 172 с.

7. Гетьман В.Г. Финансовый учет: Учебник / Под ред. В.Г. Гетьмана - 5-e изд., перераб. и доп. - М.: НИЦ Инфра-М, 2012. - 784 с.

8. Гончарова Н.М. Бухгалтерский учет. Краткий курс: учеб.пособие / Н.М. Гончарова. - М.: Форум, 2009. - 160 с.

9. Городов О.А. Правовое обеспечение инновационной деятельности: Монография / О.А. Городов. - М.: НИЦ Инфра-М, 2012. - 209 с.

10. Климова М.А. Бухгалтерский учет. Самоучитель: Учеб.пособие / М.А. Климова. - 3-e изд. - М.: ИД РИОР, 2009. - 217 с.

11. Кобозева Н.В. Банкротство: учет, анализ, аудит: Практическое пособие / Н.В. Кобозева. - М.: Магистр: НИЦ ИНФРА-М, 2013. - 208 с.

12. Кондраков Н.П. Бухгалтерский учет: Учебник / Н.П. Кондраков. - 2-e изд., перераб. и доп. - М.: ИНФРА-М, 2009. - 720 с.

13. Кондраков Н.П. Бухгалтерский учет: Учебник / Н.П. Кондраков. - 4-e изд., перераб. и доп. - М.: ИНФРА-М, 2011. - 681 с.

14. Лытневая Н.А. Бухгалтерский финансовый учет: учебное пособие / Под общ.ред. Н.А. Лытневой. - М.: ИД ФОРУМ: ИНФРА-М, 2011. - 656 с.

15. Мизиковского Е.А. Теория бухгалтерского учета: Учебник / Под общ.ред. Е.А. Мизиковского, М.В. Мельник. - 2-e изд., перераб. и доп. - М.: Магистр, 2009. - 382 с.

16. Поленова С. Н. Теория бухгалтерского учета [Электронный ресурс] : Учебник / С. Н. Поленова. - 3-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 464 с.

17. Сигитов Ю.И. Бухгалтерская (финансовая) отчетность: Учебное пособие / Ю.И. Сигидов, А.И. Трубилин, Е.А. Оксанич, М.С. Рыбянцева; Под ред. Ю.И. Сигидова. - М.: ИНФРА-М, 2012. - 366 с.

18. Терентьева Т.В. Теория бухгалтерского учета: Учебное пособие / Т.В. Терентьева. - М.: Вузовский учебник, 2008. - 208 с.

19. Шаститко А.Е Разработка концептуальных подходов к моделированию результатов гидрометеорологического обеспечения экономической деятельности/ А.Е. Шаститко, С.М. Плаксин . М.: МАКС Пресс, 2009. - 74 с.

20. Щербакова В.И. Теория бухгалтерского учета: Учебник / В.И. Щербакова. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2013. - 352 с.

ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ

СИНУСОИДАЛЬНЫХ СИГНАЛАХ

Электрический ток, изменяющийся с течением времени называется переменным. Если изменение токов и напряжений с течением времени изменяется одинаково, то такие напряжения и токи называются периодическими. Время одного полного изменения сигнала – период. Если изменения токов и напряжений происходит по закону синуса (косинуса), то такие токи и напряжения называются синусоидальными. Большинство промышленных потребителей электрической энергии работает от сети переменного синусоидального напряжения.

Параметры синусоидального тока и напряжения.

1. i, u, e – мгновенные ток, напряжение и ЭДС (указанные величины - функции времени),

2. I_m, U_m, E_m – амплитудные ток, напряжение и ЭДС,

3. T – период, с,

4. f – частота (величина обратная периоду), 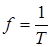, Гц,

5. 50 Гц – промышленная частота, 400 Гц – авиационная частота,

6. 12,5 Гц – электротранспортная частота, применявшаяся за рубежом,

7. угловая частота w, , рад/с,

8. y - начальная фаза, характеризует положение прохождение нулевого значения синусоидальной функцией относительно начала координат при переходе от отрицательных значений к положительным.

Если имеются два синусоидальных сигнала, например

, ,

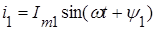то разность их начальных фаз, т.е. отставание одного сигнала от другого называется углом сдвига по фазе - j : .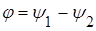

Если y₁=y₂, то j=0. Если y₁>y₂, то j>0. Если y₁<y₂, то j<0. В электротехнике обычно углом j считают угол сдвига между током на каком-либо элементе и падением напряжения на нем.

Действующие и средние значения токов и напряжений.

Среднее значение тока за период равно 0, поэтому расчет электрических цепей синусоидального тока производят по действующим значениям токов, напряжений и ЭДС. Для определения действующих значений токов и напряжений применяют энергетический подход.

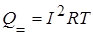- Мощность в цепи постоянного тока.

- Активная мощность в цепи переменного тока

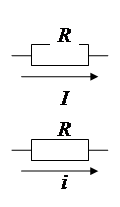
Действующее значение синусоидального тока – такое значение тока, при прохождении которого через сопротивление R выделяется такое же количество тепла, какое выделяется при прохождении постоянного тока I через такое же сопротивление R. Следовательно: ,

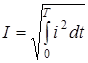, - действующее значение тока.

Если принять 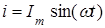, то . Аналогично .

Среднее значение тока определяется за полпериода и умножается на 2:

, .

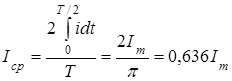Изображение синусоид комплексными числами

Синусоидальный ток постоянной частоты можно изобразить вращающимся с постоянной частотой w вектором на комплексной плоскости. Проекция этого вектора на мнимую ось равна мгновенному значению тока. Любое комплексное число можно представить в виде:

.

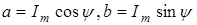
При t=0 .

При любом, произвольном t: , .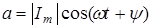

Формы записи комплексных чисел

Так как расчеты, в основном, выполняются по действующим значениям синусоидальных сигналов, то формы записи комплексных чисел представлены для действующих значений (все эти формы справедливы и для амплитудных значений).

1. Тригонометрическая форма:

2. Алгебраическая форма:

.

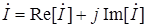3. Показательная форма

.

Комплексный метод расчета электрических цепей базируется на алгебре комплексных чисел. Арифметические действия: сложение и вычитание удобнее производить в алгебраической форме записи; умножение, деление и потенцирование - в показательной. Современные ЭВМ для расчетов используют алгебраическую форму записи комплексных чисел.

Параметры элементов электрической цепи

переменного тока

1. Приемники, в которых электрическая энергия преобразуется в тепло.

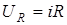
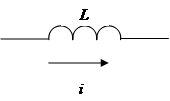2. Приемники, в которых электрическая энергия преобразуется в энергию магнитного поля (индуктивный элемент).

L – Индуктивность (Гн). Основное свойство индуктивного элемента - наведение ЭДС самоиндукции и ЭДС взаимоиндукции (при наличии индуктивно связанных катушек) при изменении потокосцепления.

В формулировке Максвелла закон электромагнитной индукции имеет следующую форму записи:

.

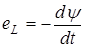y - потокосцепление – сумма магнитных потоков, сцепляющихся со всеми витками. .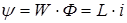

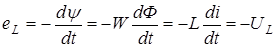
Энергия магнитного поля, выделяемая в индуктивном элементе

.

4. Емкостной элемент – элемент, в котором электрическая энергии преобразуется в энергию электрического поля.

C – Электрическая емкость (Ф, мкФ, нФ, пФ).

Основное назначение емкостного элемента – накопление электрического заряда – q.

, , .

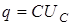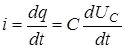Рассмотренные выше элементы - идеализированные, т.к. все три явления встречаются в одном устройстве. Если все три явления присутствуют в равной степени, то элемент заменяют схемой замещения.

Например, схема замещения катушки с учетом сопротивления провода, из которого она намотана, выглядит следующим образом.

Схема замещения конденсатора с учетом несовершенства изоляции между обкладками.

Для учета явлений, происходящих в реальных цепях, элементы цепей изображают схемами замещения, которые являются математическими моделями элементов, составленных из R, L, C элементов, и учитывающие сущность явлений.

Токи и напряжения в идеальных ЭЛЕМНТАХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ.