Сверхпроводимость

Свойство многих проводников, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охлаждении ниже определенной критической температуры Т_к, характерной для данного вещества, названо сверхпроводимостью.

Скачкообразное исчезновение сопротивление ртути при Т_к = 4,15 К впервые наблюдал голландский физик Х. Камерлинг-Оннес в 1911 г. Как выяснилось впоследствии, сверхпроводящее состояние при низких температурах свойственно примерно половине металлических элементов, большому числу металлических соединений, ряду полупроводников и оксидов. В настоящее время сверхпроводимость обнаружена у огромного числа сплавов и соединений. Измеренные значения Т_к для металлов лежат в интервале температур от нескольких тысячных долей Кельвина до 10 К. Долгое время самым высокотемпературным сверхпроводником (Т_к = 23,4 К) считали сплав NbGe. В 1986–88 г.г. сверхпроводящий переход при Т_к ≈ 120 К был обнаружен в оксидных системах типа Tl₂Ba₂Ca₂Cu₃O_x. К 2000 г. в литературе появились сообщения об обнаружении сверхпроводников с Т_к = 180 и даже 240 К.

Величина сопротивления металла в сверхпроводящем состоянии меньше 10^–22 Ом×м (для сравнения, сопротивление несверхпроводящих чистых образцов Cu или Ag составляет около 10^–11 Ом×м при температуре жидкого гелия). Сверхпроводящее состояние – особое физическое состояние вещества, не соответствующее модели «идеального» проводника с исчезающе малым сопротивлением (рис. 2.8).

В 1933 г. немецкие физики Ф.В. Мейснер (F.W. Meissner) и Р. Оксенфельд (R. Ochsenfeld) на образцах олова и свинца установили, что слабое магнитное поле не проникает вглубь сверхпроводника, т.е. при Т < Т_к магнитный поток «выталкивается» из проводника. Таким образом было показано, что в сверхпроводящем состоянии проводники становятся идеальными диамагнетиками. Идеальный диамагнетизм присущ всем сверхпроводникам при Т < Т_к. Явление, заключающееся в том, что внутри сверхпроводника магнитная индукция равна нулю, получило название эффекта Мейснера.

Исчезновение магнитного поля внутри сверхпроводника при его охлаждении ниже Т_к во внешнем магнитном поле связано с появлением в образце поверхностных токов, которые создают внутри него магнитное поле, равное по величине и противоположное по знаку внешнему полю. Результатом является полная компенсация магнитного поля внутри образца. Магнитное поле проникает только в тонкий (~10^–4÷10^–5 мм) поверхностный слой сверхпроводника. Именно в этом слое текут поверхностные экранирующие токи, а также токи, создаваемые внешним источником.

«Выталкивание» магнитного поля из сверхпроводника наблюдается только в слабых полях. Сверхпроводящее состояние разрушается, если напряженность внешнего магнитного поля превышает некоторую величину Н_к, называемую критическим магнитным полем. Эта величина уменьшается от значения Н_к0 при Т = 0 К до нуля при Т = Т_к (рис. 2.9, а).

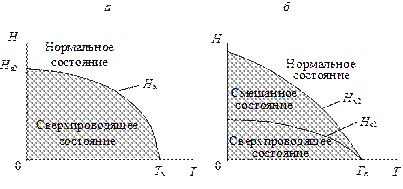
Рис. 2.9 Зависимость критического магнитного поля от температуры
сверхпроводника 1-го (а) и 2-го (б) рода

Экспериментально установлено, что напряженность критического магнитного поля сверхпроводников уменьшается с ростом температуры в соответствии с выражением:

Н_к(Т) = Н_к0 . (2.7)

Значения Н_к0 для металлических сверхпроводников лежат в интервале от нескольких десятых до нескольких единиц ампер на метр.

В достаточно сильных магнитных полях свойства сверхпроводников не одинаковы, поэтому их подразделяют на две группы – сверхпроводники первого и второго рода.

В сверхпроводники 1-го рода магнитное поле не проникает до тех пор, пока его напряженность не превысит критическое значение Н_к(Т). При весь образец возвращается в нормальное (несверхпроводящее) состояние и магнитное поле проникает в него (рис. 2.10, а). В сверхпроводниках 2-го рода существует два критических поля Н_к1(Т) и Н_к2(Т), рис. 2.9, б. При напряженности поля, меньшей нижнего критического значения Н_к1, магнитный поток не проникает в образец. Если магнитное поле превышает верхнее критическое значение Н_к2, образец переходит в нормальное состояние и поле полностью проникает в образец. В интервале полей Н_к1 < Н < Н_к2 возникает так называемое смешанное состояние, для которого характерно частичное проникновение магнитного потока в образец (рис. 2.10, б). В образце образуется сложная структура из чередующихся нормальных и сверхпроводящих областей.

Рис. 2.10 Зависимость магнитной индукции В внутри сверхпроводника

1-го рода (а) и 2-го рода (б) от напряженности Н внешнего магнитного поля: 1 – сверхпроводящее, 2 – смешанное, 3 – нормальное состояние

Природа сверхпроводимости была выяснена в 1957 г. (лишь через 46 лет после открытия этого явления) американским физиком-теоретиком Л. Купером. Согласно эффекту Купера, к сверхпроводимости металла приводит объединение электронов проводимости в пары. На основе этого эффекта американские физики Дж. Бардин, Л. Купер и Дж. Шриффер сформулировали микроскопическую теорию сверхпроводимости (модель БКШ). За ее создание они в 1972 г. были удостоены Нобелевской премии.

Согласно эффекту Купера, два электрона с противоположными спинами, в результате притяжения, вызванного колебаниями кристаллической решетки (т.е. обмениваясь фононами), могут образовать связанное состояние – куперовскую пару. Заряд такой пары (квазичастицы) равен 2е, ее спин равен нулю, т.е. является целочисленным, поэтому куперовскую пару относят к бозонам. Бозоны, в отличие от фермионов, могут находиться в состоянии с одним и тем же импульсом (или энергией). При достаточно низкой температуре происходит фазовый переход квантового газа, состоящего из бозонов, в состояние с нулевым импульсом, т.е. в бозе-конденсат. Плавление такого конденсата приводит к сверхтекучести системы (например, жидкого гелия ⁴Не). Сверхпроводимость имеет родственную природу со сверхтекучестью и представляет собой «сверхтекучесть» куперовских электронных пар, образовавшихся в металле.

Сверхпроводники первого рода утрачивают сверхпроводимость скачком (фазовый переход I рода) при достижении соответствующей данному магнитному полю критической температуры T_к(Н) либо при повышении напряженности внешнего поля до критического значения Н_к(Т). Критическое поле имеет простое термодинамическое истолкование: оно определяет разность удельных (на единицу объема) свободных энергий сверхпроводящей и нормальной фаз:

(2.8)

По измеренной зависимости Н_к(Т) с помощью формулы (2.8) могут быть рассчитаны все термодинамические характеристики сверхпроводника 1-го рода. В частности, удельная теплота фазового перехода в сверхпроводящее состояние

где S_н и S_c – удельные энтропии соответствующих фаз. Скачок удельной теплоемкости при T = T_к равен

Согласно модели БКШ, критическое поле связано с критической температурой соотношением:

(где p_F и v_F – импульс и скорость электрона вблизи уровня Ферми), а его температурная зависимость в предельных случаях имеет вид:

.

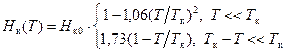Обе последние формулы близки к эмпирическому соотношению (2.7), которое хорошо описывает экспериментальные данные (рис. 2.9, а).

Сила притяжения между электронами, приводящая к образованию куперовских пар, зависит от многих факторов. Тем не менее, у всех известных сверхпроводников эти силы определяются взаимодействием электронов с фононами. Развитие теории сверхпроводимости стимулировало поиски других механизмов реализации этого явления в конденсированных телах. Особое внимание уделено так называемым нитевидным, слоистым и сэндвичевым структурам, обладающим экситонной проводимостью, в которых можно ожидать более интенсивного притяжения между электронами, чем в обычных сверхпроводниках, а, следовательно, − и более высокой температуры перехода в сверхпроводящее состояние.

Практическое применение сверхпроводимости непрерывно расширяется. На использовании свойств сверхпроводников основан принцип действия сверхпроводящих магнитов, магнитометров, резонаторов, элементов ЭВМ и др. Перспективы применения эффекта сверхпроводимости связаны с разработкой высокотемпературных сверхпроводников (Т_к ~ 300К), которые могли бы совершить переворот в технике.

Эффект Джозефсона.Протекание сверхпроводящего тока возможно через тонкий слой диэлектрика, разделяющий два сверхпроводника (так называемый джозефсоновский контакт). Этот эффект, предсказанный английским физиком, Нобелевским лауреатом (1973 г.) Б. Джозефсоном (B. Josephson) в 1962 г., был экспериментально обнаружен в 1963 г. Электроны проводимости проходят через диэлектрик (например, пленку оксида металла толщиной порядка10⁻⁹ м) благодаря туннельному эффекту. Если ток через контакт не превышает критического значения I_к, то падение напряжения на контакте отсутствует (стационарный эффект Джозефсона). Если пропускать ток, больший критического, то на контакте возникает падение напряжения, и он излучает электромагнитные волны (нестационарный эффект Джозефсона). Частота излучения ν связана с падением напряжения U соотношением

ν = 2еU/ h, (2.9)

где е – заряд электрона, h – постоянная Планка. Излучение вызвано тем, что куперовские пары, создающие сверхпроводящий ток, при переходе через контакт Джозефсона приобретают избыточную по отношению к основному состоянию энергию 2еU. Единственная возможность для пары электронов вернуться в основное состояние − это излучить квант электромагнитной энергии hν = 2eU. Таким образом, переменное электромагнитное поле, а значит и переменный ток через контакт, возникают под действием постоянного электрического поля (приложенного напряжения U).

Согласно модели БКШ, куперовские пары электронов характеризуются единой волновой функцией, фаза j которой плавно меняется. Иными словами, имеет место фазовая когерентность сверхпроводящих электронов (колебания называются когерентными, если разность их фаз остается постоянной или закономерно изменяется во времени и при сложении колебаний определяет амплитуду суммарного колебания). При прохождении сверхпроводящих электронов через несверхпроводящую диэлектрическую прослойку фазовая когерентность частично нарушается и происходит скачок фазы , где j₂ и j₁ – фазы волновой функции в сверхпроводниках по обе стороны от прослойки. Согласно квантовомеханическим представлениям, ток, протекающий через прослойку, должен быть пропорционален разности фаз:

. (2.10)

Экспериментальное обнаружение этого тока доказывает, что в природе существуют макроскопические явления, непосредственно определяемые фазой волновой функции электрона. Из формулы (2.10) видно, что ток через джозефсоновский контакт не может превысить I_к.

Величина I_к и механизм прохождения электронов через прослойку зависят от электрических свойств материала прослойки (диэлектрик, полупроводник, металл в нормальном состоянии). Типичный пример джосефсоновского контакта – туннельный контакт, состоящий из двух металлических электродов – одинаковых или различных пленочных сверхпроводников, разделенных очень тонким слоем (~ 10 ÷ 20 Å) диэлектрика, например, оксидом металла одного из электродов.

На рис. 2.11 приведена типичная вольтамперная характеристика туннельного контакта одинаковых сверхпроводников. При I = I_к происходит переход из стационарного в нестационарный режим. При последующем уменьшении тока нестационарный режим может сохраняться даже при значениях тока, значительно меньших критического, т.е. в туннельном контакте проявляется гистерезис.

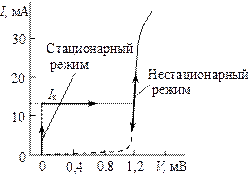
Рис. 2.11 Вольтамперная характеристика туннельного контакта Sn–Sn при температуре 1,4 К. Прослойка – пленка оксида олова; стрелками показано направление изменения

При нестационарном эффекте Джозефсона разность фаз на контакте зависит от времени:

. (2.11)

Уравнение (2.11) является следствием уравнения Шрёдингера для волновой функции пары сверхпроводящих электронов при наличии постоянного потенциала U и не связано с существованием прослойки между двумя сверхпроводниками, т.е. имеет общий характер. Соотношения (2.9) и (2.11) называют соотношениями Джозефсона.

Кроме туннельного контакта эффект Джозефсона наблюдается в структурах, где между сверхпроводниками находится тонкий слой полупроводника или металла в нормальном состоянии. Такие системы, как и джозефсоновский контакт, называют слабосвязанными сверхпроводниками.

Эффект Джозефсона подтверждает основную концепцию современной теории сверхпроводимости – наличие единой волновой функции и фазовой когерентности спаренных электронов в сверхпроводящем состоянии. Благодаря относительной простоте и доступности эксперимента этот эффект представляет собой одну из уникальных возможностей изучать проявление квантовых свойств микромира в макроскопическом масштабе.

Эффект Джозефсона используют в криогенных приборах, в частности, в сверхпроводящих квантовых интерферометрах – сквидах (от англ. аббревиатуры SQUID – Superconducting Quantum Interference Device). С помощью сквидов могут быть измерены предельно малые величины: напряженности магнитного поля – 10^-12 А/м, тока – 10^-10 А, напряжения – 10^-15 В. Джозефсоновские контакты применяют в качестве генераторов и детекторов излучения СВЧ-диапазона. На основе сквидов разрабатываются быстродействующие элементы памяти, логические устройства компьютеров и другие электронные приборы нового поколения.