Элементы теории

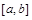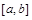В вычислительной практике часто возникает задача восстановления функции на отрезке , если известны ее значения в отдельных фиксированных точках отрезка. Такая задача имеет место при табличном задании функции. Значения в этом случае – продукт измерения физической величины на наборе аргумента . Чтобы приближенно восстановить функцию на всем отрезке , строят аппроксимирующую функцию , расчеты по которой в определенном смысле приближаются к экспериментально полученным значениям.

К табличному заданию функции прибегают также в том случае, когда аналитический вид функции известен, но сложен и требует большого объема вычислений для определения ее отдельных значений. Над такой функцией, кроме того, трудно выполнить математические операции дифференцирования и интегрирования. Замена приближенной функцией позволяет упростить вычисления. Для этого по известному выражению вычисляют небольшую таблицу ее значений и по ним, как и ранее, строят аппроксимирующую функцию .

В качестве аппроксимирующей функции наиболее часто используют степенной полином

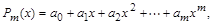(4.1)

при этом порядок полинома . Такую аппроксимацию называют полиномиальной. Она очень удобна, так как степенные полиномы просты по форме, легко вычисляются, дифференцируются и интегриру- ются.

Для периодической функции в качестве выбирают тригонометрические многочлены. Если аппроксимируемая функция обращается в бесконечность в заданных точках или вблизи них, то строят в классе рациональных функций.

Рассмотрим теперь, как вычисляются коэффициенты в (4.1) при полиномиальной аппроксимации. Если значения заданы точно, то коэффициенты выбираются таким образом, чтобы значения полинома в точках совпадали с заданными значениями . Такую аппроксимацию назы-вают интерполяцией. Порядок полинома при интерполяции однозначно определяется количеством узлов интерполяции (так называют точки ):

.

Искомые коэффициенты полинома являются решением системы

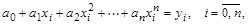
число уравнений в которой совпадает с количеством неизвестных коэффициентов и узлов интерполяции.

При табличном задании функции приближенными значениями, полученными из эксперимента, не имеет смысла привлекать интерполяцию и требовать совпадения и в точках . Ошибки измерения функции в узловых точках будут внесены в интерполяционный полином и исказят истинную картину ее поведения. Как показывает практика, в этом случае лучше аппроксимируют функции, построенные по методу среднеквадратического приближения.

При среднеквадратическом приближении за меру близости функций и принимается величина

,

где – заданная неотрицательная весовая функция, учитывающая неодинаковую точность измерения в точках .

Метод среднеквадратического приближения функций, заданных набором экспериментальных данных, называется методом наименьших квадратов (МНК). МНК широко используется для обработки результатов измерения, оценки параметров известной зависимости, подбора вида зависимости, сглаживания и дифференцирования результатов наблюдений, идентификации и оценки параметров систем.

Рассмотрим применение метода наименьших квадратов для среднеквадратического приближения функции полиномом степени 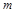. Пусть – приближенные значения функции в точках . Среди многочленов степени найдем многочлен, обеспечивающий минимум выражению

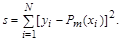
Для определения значений коэффициентов полинома, обращающих в минимум, приравняем к нулю частные производные от по т. е.

(4.2)

После несложных преобразований соотношений (4.2) получим систему линейных алгебраических уравнений – го порядка (эти уравнения называют нормальными) относительно неизвестных коэффициентов : (4.3)

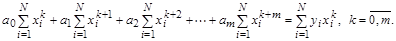
Анализ системы (4.3) свидетельствует о том, что для ее формирования необходимо вычислить и запомнить в одномерном массиве 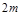сумм вида

, (4.4)

являющихся значениями коэффициентов нормальных уравнений, и таких сумм, как

,

представляющих правые части этих уравнений. Используя элементы одномерного массива, хранящего суммы (4.4), нетрудно сформировать матрицу коэффициентов системы (4.3), учитывая, что матрица коэффициентов имеет одинаковые значения вдоль каждой восходящей диагонали.

Коэффициенты вычисляются путем решения системы линейных алгебраических уравнений (4.3), например, методом Гаусса. Являясь функцией случайных величин 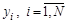, эти коэффициенты также будут случайными, т. е. полученные значения будут только оценками истинных значений. Для того, чтобы найти их точность, необходимо определить числовые характеристики их законов распределений.

Качество МНК-аппроксимации принято характеризовать остаточной дисперсией

(4.5)

где – число степеней свободы. Из (4.5) следует, что из наблюдений для определения коэффициентов полинома с помощью условных уравнений (4.3) достаточно использовать только наблюдений. Остальные 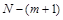наблюдения используются для уточнения оценок коэффициентов, т. е. уменьшения их рассеяния вокруг истинного значения – математического ожидания и уменьшения степени их взаимосвязи – коэффициентов ковариации, отражающих то обстоятельство, что оценки получены по одному и тому же статистическому материалу.

Замечание. Метод наименьших квадратов наиболее просто применить, когда искомые параметры входят в аппроксимирующую зависимость линейно. Более сложные приближающие функции сводят к многочленным путем замены переменных (если это возможно). Например, зависимость преобразуют к заменой .