Описание алгоритма

Алгоритм МНК-аппроксимации реализуется следующим образом:

Алгоритм 4.1

1. Ввести табличные данные (если аппроксимирующая функция нелинейна относительно коэффициентов аппроксимации, то предварительно следует линеаризовать ее путем походящей замены переменных).

2. Ввести число измерений и степень аппроксимирующего полинома

3. Вычислить суммы 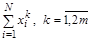и разместить их в одномерном массиве размером .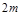

4. Сформировать матрицу коэффициентов 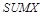размером путем выполнения операции присваивания:

5. Сформировать правые части системы (4.3) по правилу:

6. Определить коэффициенты , решив методом Гаусса сформированную систему (4.3).

7. Вычислить по соотношению (4.5) остаточную дисперсию и на этой основе среднеквадратическое отклонение .

8. Пересчитать коэффициенты, если это необходимо для перехода к исходной нелинейной аппроксимирующей функции , и напечатать их.

9. Вывести в графическом виде построенную функцию .