Случайные величины.

12.2.1. Случайная величина Х равна числу появлений «герба» в серии из n+3 бросаний монеты. Найти закон распределения и функцию распределения F(x) этой случайной величины; вычислить ее математическое ожидание MXи дисперсию DX; построить график F(x).

12.2.2. Закон распределения дискретной случайной величины X имеет вид:

Найти вероятности p₄, p₅, и дисперсию DX, если математическое ожидание MX=-0,5+0,5m+0,1n.

12.2.3. Плотность распределения непрерывной случайной величины X имеет вид:

Найти:

а) параметр а; б) функцию распределения ;

в) вероятность попадания случайной величины X в интервал

;

г) математическое ожидание MX и дисперсию DX.

Построить график функци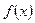й и .

12.2.4. Случайные величины имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξ_i=m+n, а дисперсия Dξ₁=n²/3. Найти вероятности: а) ; б) ; в) .