Дифференциальное исчисление.

Пределы, непрерывность и разрывы функций.

3.1.1.Найти пределы функций:

а) ;

б) ;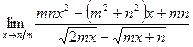

в) ;

г) .

3.1.2.В точках и для функции 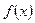установить непрерывность или определить характер точек разрыва. Нарисовать график функции 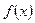в окрестностях этих точек:

;

Производные функций.

3.1.3.Найти производные 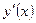функций:

а) ; б) ;

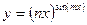в) ; д) ; е) ;

ж)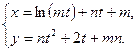

Приложения производной.

3.2.1.С помощью методов дифференциального исчисления построить график функции .

Приближенное решение алгебраических уравнений.

3.3.1.Для уравнения отделить положительный корень и найти его приближенно с точностью :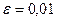

а) методом деления отрезка пополам;

б) методом касательных.

Примечание. Можно считать, что точность достигнута, если разность между соседними приближениями и удовлетворяет неравенству .

Интегральное исчисление.