Основные положения. Связи необходимые и дополнительные.

Для решения задач сопротивления материалов необходимо знать все внешние силы, действующие на конструкцию, включая реакции наложенных на нее связей. Из теоретической механики известно, что для равновесия твердого тела, нагруженного плоской системой сил, достаточно наложить на тело три связи, а нагруженного пространственной системой сил – шесть связей. Соответственно для таких систем можно составить три и шесть независимых уравнений равновесия. Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления можно определить с помощью уравнений равновесия, без использо­вания дополнительных условий, то такая система называется ста­тически определимой.

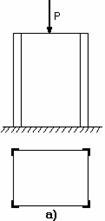
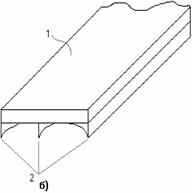
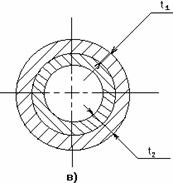
Рис. 2.36

Примерами таких конструкций могут быть: армированные уголками стойки (рис.2.36, а); панель крыла самолета, состоящая из обшивки 1 с продольными ребрами 2 (рис. 2.36, б); составной цилиндр, полученный пу­тем напряженной посадки двух труб из различных материалов (рис. 2.36, в). В других случаях, с целью повышения жесткости и надежности сис­темы, вводятся дополнительные связи сверх тех минимально необходи­мых, которые обеспечивают ее кинематическую неизменяемость. Нало­жение на систему дополнительных связей превращает ее в статически неопределимую. Напомним, что кинематическая неизменяемость пло­ской системы обеспечивается тремя, а пространственной – шестью свя­зями.

Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. Лишними такие связи называются только потому, что они не являются необходимыми для обеспечения равновесия конст­рукции и ее геометрической неизменяемости, хотя постановка их дикту­ется условиями эксплуатации. По условиям прочности и жесткости кон­струкции лишние связи могут оказаться необходимыми.

В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.

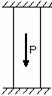
а) б) в)

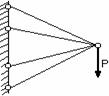
Рис. 2.37

На рис.2.37 приведены схемы 3-х плоских систем с «лишними» связями: а – стержневой подвески; б – стержня, закрепленного обоими концами; в – стержневого кронштейна. В схеме, показанной на рис. 2.37, в, вся система состоит из упругих звеньев. Подсчет числа наложенных связей произво­дится в этом случае следующим образом. Каждый стержень связан с опорной поверхностью двумя связями. Всего таких связей 8. Шарнир, соединяющий концы стержней, снимает связи, ограничивающие относи­тельный или взаимный их поворот. При соединении двух стержней од­ним шарниром снимается одна связь, трех стержней – две связи, четырех – три и т.д. В данном случае снимаются три связи. Следовательно, всех связей, наложенных на эту систему оказывается пять, две из которых мо­гут считаться «лишними».

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. За­ключаются они в том, что в элементах статически неопределимых систем напряжения возникают не только от действия внешних сил, но и в ре­зультате изменения температуры, неточности изготовления деталей, не­точностей их сборки, смещения мест опорных креплений и ряда других причин. Объясняется это тем, что деформация одного из элементов в статически неопределимой системе приводит к деформа­ции и других ее элементов.

Например, если один из стержней системы (рис. 2.37, в) изготовлен по длине неточно, то соединение концов стержней одним шарниром возможно только путем деформации всех стержней.

Сила, возникающая при деформации одного из стержней, вызывает усилия в других стержнях, находящихся с ним в шарнирном соединении. Смонтированная система приходит в равновесие, следовательно, сово­купность сил системы обеспечивает ее равновесие. Эти силы вызывают соответствующие, называемые начальными, напряжения в стержнях.

В статически неопределимых конструкциях при изменении темпера­туры ее элементов по сравнению с температурой, при которой осуществ­лялась сборка, возникают дополнительные усилия и напряжения, кото­рые принято называть температурными.

Распределение усилий между элементами системы зависит от их же­сткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живуче­стью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис. 2.37, в не приводит к потере способности восприни­мать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.