Степень статической неопределимости. Методика ее определения.

Статически неопределимые системы характеризуются степенью ста­тической неопределимости, которая равна числу «лишних» связей и мо­жет быть вычислена как разность между числом неизвестных сил и чис­лом независимых уравнений равновесия. По числу единиц этой разности системы бывают 1,2,3….n раз статически неопределимыми.

Для расчетов составляется силовая схема заданной системы, на которой указываются все известные и неизвестные силовые факторы.

При составлении силовой схемы в случае определения внутренних силовых факторов применяется метод сечений, согласно которому каждое звено системы разделяется на две части в произвольном сечении, затем отбрасываются части, примыкающие к опорным элементам, а их действие на оставшиеся части заменяется продольными силами. После этого на схеме показываются все заданные внешние силы и реакции опор.

Затем по этой схеме устанавливается возможное число независимых уравнений равновесия. Степень статической неопределимости подсчитывается, как разность между числом неизвестных сил и числом независимых уравнений равновесия.

На рис.2.38, а изображен кронштейн, состоящий из двух стерж­ней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система яв­ляется плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла 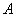, т.е.

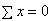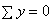, . (2.37)

Раскрывая эти уравнения, получаем замкнутую систему линей­ных уравнений относительно неизвестных усилий N₁ и N₂ в кото­рой количество уравнений равно количеству неизвестных:

; .

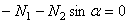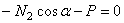Если конструкцию крон­штейна усложнить, добавив еще один стержень (рис.2.38, б), то усилия в стержнях N₁, N₂ и N₃ прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.37) имеются уже три неиз­вестных усилия в стержнях. В таких случаях говорят, что сис­тема один раз статически неопределима.

Рис.2.38

На рис.2.39 приведены примеры статически неопределимых систем. В стержне с жестко заделанными концами (рис.4.2, а) возникают две реакции, а уравнение равновесия можно составить только одно, следовательно, конструкция один раз статически неопределима. Не нарушая равновесия стержня, можно отбросить одну из опор.

Рис.2.39

Для системы из трех стержней (рис.2.39, б) можно составить два уравнения равновесия, а неизвестных сил в системе три, следовательно, система один раз статически неопределима. Один из стержней не нужен для равновесия системы, и его можно отбросить. Рассуждая аналогично, можно установить, что система из четырех стержней (рис.2.39, в) дважды статически неопределима.

Для определения внутренних сил в системе из пяти стержней (рис.2.39, г) необходимо вырезать и рассмотреть раздельно равновесие узлов 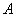и . К каждому узлу примыкают три стержня (всего пять стержней и, следовательно, пять неизвестных сил), а уравнений равновесия для каждого узла можно составить два, т.е. всего четыре уравнения. Система один раз статически неопределима.

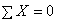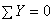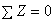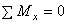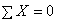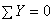Напомним, что для пространственной системы сил можно составить шесть независимых уравнений равновесия: три уравнения, выражающие сумму проекций всех сил на три взаимно перпендикулярные оси ( , , ), и три - сумму моментов всех сил относительно этих же осей ( , , ). Для общего случая сил, лежащих в одной плоскости- три независимых уравнения (например: , , ). В частных случаях плоской системы можно составить два независимых уравнения равновесия: для системы параллельных сил (например: 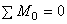, 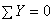) и для системы сил, линии действия которых пересекаются в одной точке ( 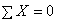, 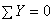). Для сил, линии действия которых лежат на одной прямой, можно записать только одно независимое уравнение (например: ).

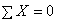На рис. 2.40 показаны примеры составления силовых схем и определения степени статической неопределимости по формуле

,

где n - общее число неизвестных сил, включая реакции опор; m - число возможных для данной системы независимых уравнений статики.

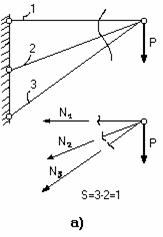
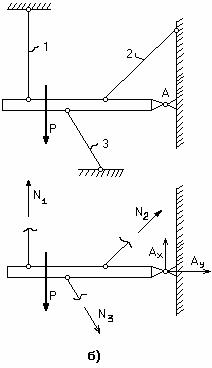
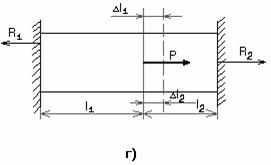
Рис.2.40