Расчет устойчивости основания устоя против сдвига по круглоцилиндрическим поверхностям скольжения

При больших нагрузках на основание может произойти потеря его устойчивости. Проверки возможной потери устойчивости основания в практике проектирования обычно выполняют посредством сдвига части основания по круглоцилиндрической поверхности скольжения. Поскольку положение наиболее опасной с точки зрения возможности сдвига поверхности скольжения заранее неизвестно, приходится выполнять проверки для нескольких поверхностей скольжения. Такой расчет очень трудоемок. В курсовой работе расчет устойчивости основания выполняется в сокращенном объеме и с некоторым упрощениями. В учебных целях считается достаточным выполнить проверку устойчивости основания устоя только для трех поверхностей скольжения. Кроме того, ширина сдвигаемой части основания назначается по условной схеме, а взаимодействие боковых (вертикальных) поверхностей сдвигаемой части с остальным грунтовым массивом не учитывается, что идет в запас устойчивости.

Следует заметить, что точность решения задачи об устойчивости основания методом круглоцилиндрических поверхностей скольжения, как и при использовании любых графоаналитических методов, во многом зависит от принятого масштаба и аккуратности исполнения расчетной схемы.

Проверка устойчивости основания на сдвиг по круглоцилиндрической поверхности скольжения выполняют в следующей последовательности.

На расчетной схеме, выполненной в масштабе не мельче 1:200, с помощью циркуля проводится из выбранного центра вращения след круглоцилиндрической поверхности скольжения. Выделенный этой линией из грунтового основания сегмент делится на несколько отсеков вертикальными плоскостями, подсчитываются объемы V_i этих отсеков и их вес F_i. Разрешается размеры выделенных отсеков снимать непосредственно с чертежа, а дуги линий скольжения заменять хордами.

Устойчивость основания против сдвига по круглоцилиндрической поверхности оценивается величиной коэффициента запаса устойчивости

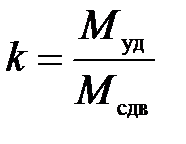, (5.1)

где М_уд и М_сдв– моменты удерживающих и сдвигающих сил относительно выбранного центра вращения.

Для определения моментов М_уд, и М_сдв рассмотрим два отсека: один из левой части сегмента, другой из правой (рисунок 5.1).

Рисунок 5.1 –Схема сил, действующих на поверхностях скольжения отсеков из левой и правой частей сегмента сдвига

Разложив силу веса отсека F_i на нормальную N_i и касательную Q_i составляющие, будем иметь:

(5.2)

где α_i – абсолютная величина угла между вертикалью из центра вращения и радиусом, проведенным в центр дуги (хорды) скольжения i-го отсека.

Силы F_i от веса i-ro отсека определяются по формуле (5.3).

, (5.3)

где V_i – объем i-го блока, вычисленный с учетом, его угловой ширины, показанной на рис. 5.3:

(5.4)

где A_i – площадь продольного сечения блока (по длине а на рис. 5.2);

b_i – ширина , определяется по формуле (5.5)

, (5.5)

где h_i означает высоту i–гo отсека в средней части его длины.

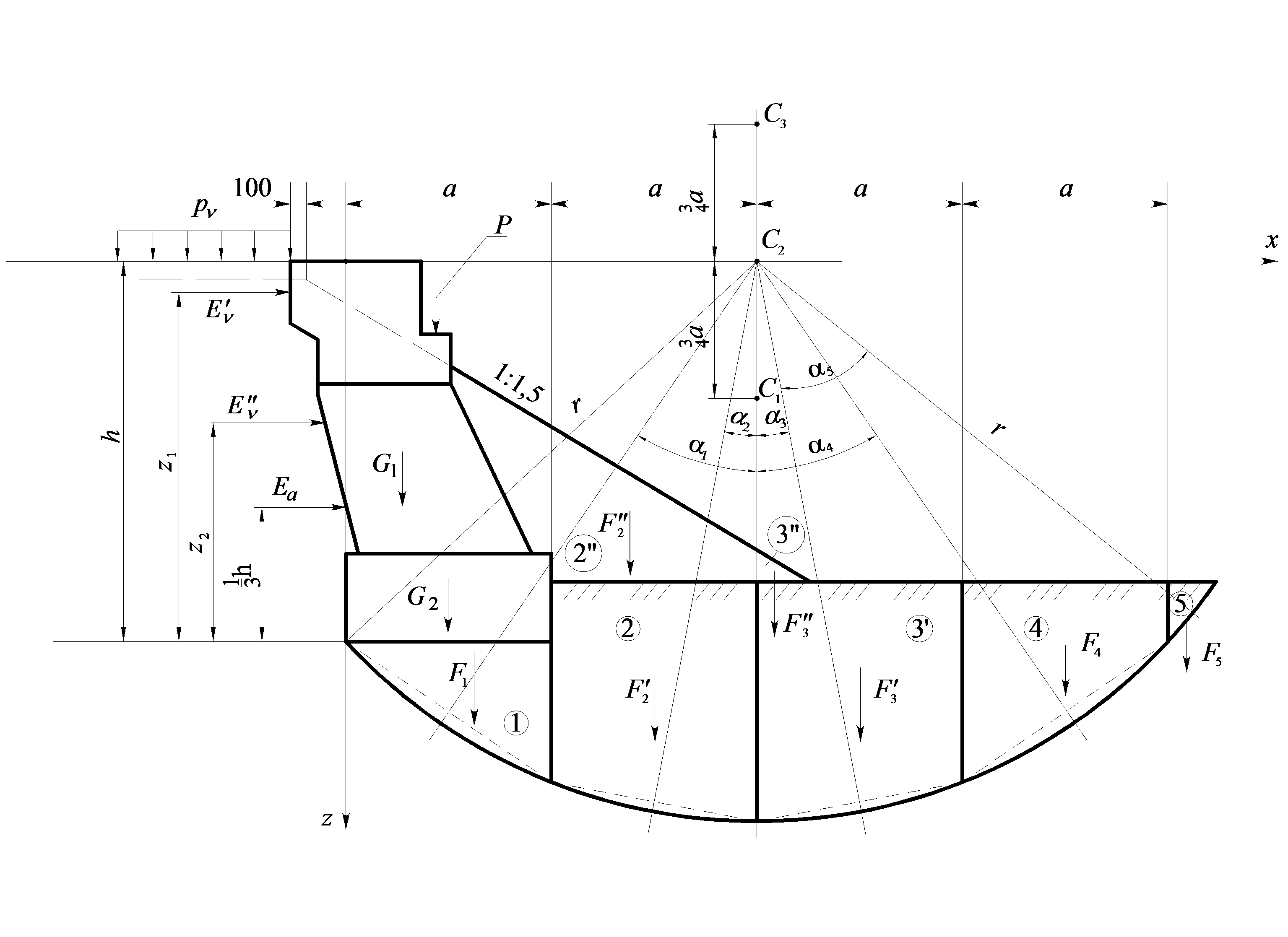
Рисунок 5.3 – Схема к расчету устойчивости основания устоя

Отметим, что на поверхность скольжения первого отсека, действует не только его собственный вес F₁но и нагрузки от устоя, т. е

(5.6)

Рисунок 5.4 – Поперечные сечения сегмента скольжения: а – а – поверхности скольжения; 1 – 2 – 3 – 4 – поперечное сечение i-го отсека в сдвигаемом сегменте основания

Кроме того,

, (5.7)

а возможно, и

, (5.8)

где и – нагрузки от веса конуса насыпи на отсеках 2и 3соответственно:

(5.9)

Здесь и – объемы участков конуса насыпи над отсеками 2и3. Отметим также и то, что сила Q_i в левом отсеке стремится сдвинуть сегмент, а в правом отсеке эта сила пре­пятствует сдвигу. Сдвигу препятствуют также и силы трения на поверхности скольжения, которые по закону Кулона равны

(5.10)

где l_i – длина дуги (хорды) линии скольжения i-го отсека. Тогда моменты удерживающих и сдвигающих сил относительно рассматриваемого центра вращения выразятся следующим образом:

; (5.11)

, (5.12)

где r – радиус круглоцилиндрической поверхности сдвига.

Вычисленный по найденным М_уди М_сд, коэффициент запаса устойчивости k характеризует, разумеется, этот запас применительно только к рассмотренной поверхности скольжения. Но очевидно и то, что через заднее ребро фундамента устоя можно провести множество круглоцилиндрических поверхностей скольжения из разных центров вращения, положение которых на плоскости чертежа будет определяться различными значениями координат х_с, z_с. Каждой из этих поверхностей скольжения соответствует свой коэффициент запаса устойчивости основания.

Условие устойчивости основания устоя против сдвига на круглоцилиндрической поверхности записывают в следующем виде:

, (5.13)

где – минимальное значение коэффициента запаса устойчивости, определенное по координатам центров вращений х_с, z_c; γ_n, определяется:

(5.14)

В курсовой работе достаточно выполнить расчеты для трех центров вращения с координатами при х_с=2а (рисунок 5.3) и определить для каждого из них свой коэффициент запаса устойчивости: k₁, k₂, k₃. Если при этом окажется, что k₂ меньше k₁ и k₃, то с помощью графика изменения k_i построенного по найденным его значениям, находим относительный минимум k_min.