
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 1. студентка 1 курса, группы Диз-Дб-1 Сабанина Анастасия.
Преподаватель: Шайкин А.Н.
Работу выполнила:
студентка 1 курса, группы Диз-Дб-1
Сабанина Анастасия.
Москва 2014.
Часть I. Рост.
| Таблица 1.1 | ||||
| № | Имя | Рост | Вес | |
| Анна | ||||
| Дарья | ||||
| Олеся | ||||
| Людмила | ||||
| Софья | ||||
| Христина | ||||
| Зинаида | ||||
| Полина | ||||
| Мария | ||||
| Эльза | ||||
| Маргарита | ||||
| Татьяна | ||||
| Барбара | ||||
| Прасковья | ||||
| Зоя | ||||
| Евдокия | ||||
| Юлия | ||||
| Нина | ||||
| Ульяна | ||||
| Ирина | ||||
| Роза | ||||
| Надежда | ||||
| Инна | ||||
| Виктория | ||||
| Раиса | ||||
| Наталья | ||||
| Яна | ||||
| Елизавета | ||||
| Фаина | ||||
| Клавдия | n1=26 | |||
| Нонна | n2=30 | |||
| Светлана | n3=35 | |||
| Жанна | n4=5 | |||
| Лариса | n5=12 | |||
| Галина | n6=20 | |||
| Ольга |
| Таблица 1.2 | ||
| № | Имя | Рост |
| Анна | ||
| Дарья | ||
| Олеся | ||
| Людмила | ||
| Христина | ||
| Зинаида | ||
| Полина | ||
| Мария | ||
| Эльза | ||
| Маргарита | ||
| Барбара | ||
| Прасковья | ||
| Зоя | ||
| Евдокия | ||
| Юлия | ||
| Нина | ||
| Ульяна | ||
| Роза | ||
| Надежда | ||
| Инна | ||
| Виктория | ||
| Раиса | ||
| Яна | ||
| Елизавета | ||
| Фаина | ||
| Нонна | ||
| Светлана | ||
| Жанна | ||
| Лариса | ||
| Ольга |
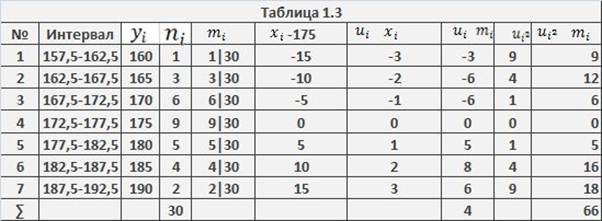
M(uᵢ)=  = -
= -  = - 0,1333
= - 0,1333
 = M(xᵢ) = M(uᵢ)·5+175=
= M(xᵢ) = M(uᵢ)·5+175=
=(-0.1333)·5+175=174.3335
Dв(uᵢ)= 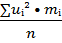 – M(uᵢ)²=
– M(uᵢ)²= 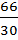 –
–
(-0.1333)²=2,1823
Dв(X)=Dв(uᵢ)·5²=2,1823·25=54,5575
Sx²= Dв(X)· 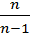 =54,5575·
=54,5575·  =56,4387
=56,4387
Sx=  =7,5125
=7,5125
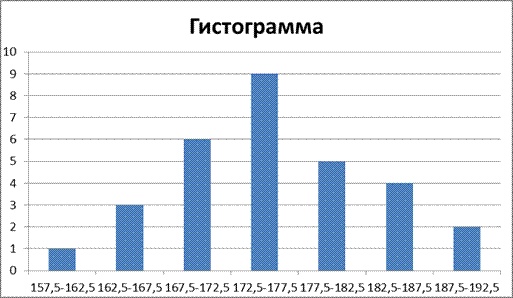
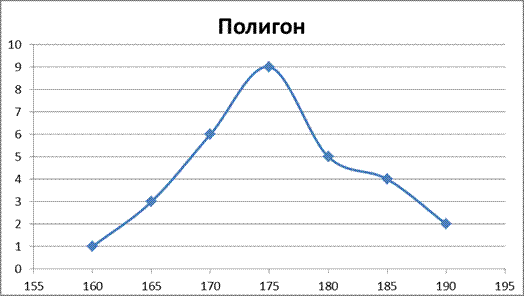


Расчёт интервальных оценок
1) Математическое ожидание
 -
- 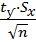 <M(x)<
<M(x)<  +
+ 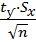 ; tу=2.045, n=30
; tу=2.045, n=30
174.3335- 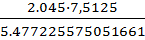 <M(x)< 174.3335+
<M(x)< 174.3335+ 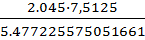
174.3335- 2,804911<M(x)< 174.3335+2,804911
171,5286<M(x)< 177,1384
2) Дисперсия
Sx(1- q) < Sx <Sx(1+q); q=0.28
7,5125 (1-0.28) < S(x) <7,5125 (1+0.28)
5,409< S(x) < 9,616
Проверка гипотезы о нормальном распределении
Таблица 1.4

 , где h=5 – длина интервала, а n=30 – количество девушек
, где h=5 – длина интервала, а n=30 – количество девушек
ϕ(uᵢ) определяем по таблице значений функции 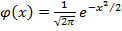
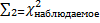 =1,5600
=1,5600
α=1-γ= 1 - 0,95 = 0,05
k-число степеней свободы: k=S-3=7-3=4
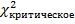 =
= 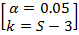
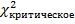 =
= 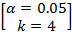
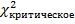 =9.5
=9.5
1,5600< 9,5 => 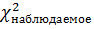 <
< 
Вывод: Так как 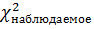 <
<  ,с уверенностью 95% нет основания отвергнуть гипотезу о нормальном распределении.
,с уверенностью 95% нет основания отвергнуть гипотезу о нормальном распределении.
Часть II. Вес.
| Таблица 2.1 | ||
| № | Имя | Вес |
| Анна | ||
| Барбара | ||
| Елизавета | ||
| Евдокия | ||
| Виктория | ||
| Лариса | ||
| Людмила | ||
| Жанна | ||
| Полина | ||
| Мария | ||
| Прасковья | ||
| Зинаида | ||
| Маргарита | ||
| Зоя | ||
| Дарья | ||
| Нина | ||
| Ульяна | ||
| Роза | ||
| Надежда | ||
| Раиса | ||
| Нонна | ||
| Инна | ||
| Юлия | ||
| Фаина | ||
| Светлана | ||
| Ольга | ||
| Олеся | ||
| Христина | ||
| Эльза | ||
| Яна |
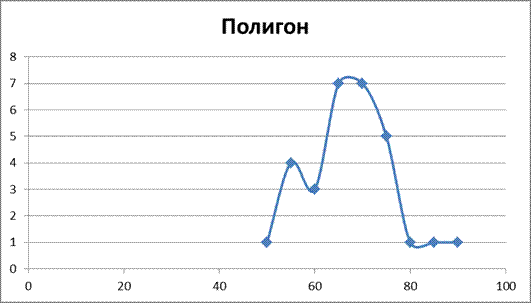
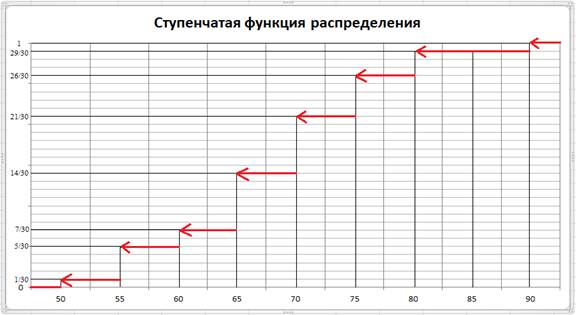
Таблица 2.2
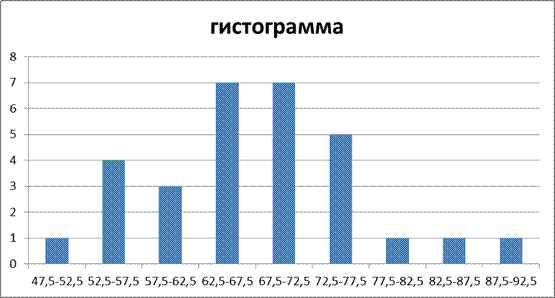
| № | Интервал | yᵢ | nᵢ | nᵢ/n | yᵢ-70 | vᵢ=(yᵢ-70)/5 | vᵢ · nᵢ | vᵢ² | vᵢ² · nᵢ |
| 47,5-52,5 | 1/30 | -20 | -4 | -4 | |||||
| 52,5-57,5 | 4/30 | -15 | -3 | -12 | |||||
| 57,5-62,5 | 3/30 | -10 | -2 | -4 | |||||
| 62,5-67,5 | 7/30 | -5 | -1 | -7 | |||||
| 67,5-72,5 | 7/30 | ||||||||
| 72,5-77,5 | 5/30 | ||||||||
| 77,5-82,5 | 1/30 | ||||||||
| 82,5-87,5 | 1/30 | ||||||||
| 87,5-92,5 | 1/30 | ||||||||
| ∑ | -13 |
n=30, средний интервал=70
M(vᵢ)= 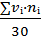 = -
= - 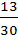 = - 0.4333
= - 0.4333
 = M(yᵢ) = M(vᵢ)·5+70=
= M(yᵢ) = M(vᵢ)·5+70=
=(-0.4333)·5+70= 67,8333
Dв(vᵢ)=  – M(vᵢ)²=
– M(vᵢ)²= 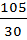 –
–
(-0.4333)²=3,3122
Dв(Y)=Dв(vᵢ)·5²=3,3122·25=82,8062
Sy²= Dв(Y)· 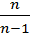 =82,8062·
=82,8062·  =85,6615
=85,6615
Sy=  =9,2553
=9,2553

Расчёт интервальных оценок
1) Математическое ожидание
 -
- 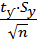 <M(x)<
<M(x)<  +
+ 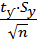 ; tу=2.045, n=30
; tу=2.045, n=30
67,8333- 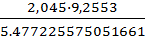 <M(x)< 67,8333+
<M(x)< 67,8333+ 
67,3333- 3,45561391<M(x)< 67,3333+3,45561391
63,8776<M(x)< 70,7889
2) Дисперсия
Sy(1- q) < Sy <Sy(1+q); q=0.28
9,2553(1-0.28) < S(x) <9,2553(1+0.28)
6,6638< Sy < 11,8467
Проверка гипотезы о нормальном распределении
Таблица 2.3

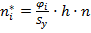 , где h=5 – длина интервала, а n=30 – количество девушек
, где h=5 – длина интервала, а n=30 – количество девушек
ϕ(vᵢ) определяем по таблице значений функции 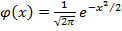
 =4.5685
=4.5685
α=1-γ= 1 - 0,95 = 0,05
k-число степеней свободы: k=S-3=9-3=6
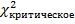 =
= 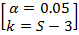
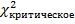 =
= 
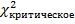 =12,6
=12,6
4.5685< 12,6=> 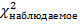 <
< 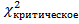
Вывод: Так как 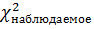 <
<  ,с уверенностью 95% нет основания отвергнуть гипотезу о нормальном распределении.
,с уверенностью 95% нет основания отвергнуть гипотезу о нормальном распределении.
Часть III. Корреляционная таблица.
Таблица 3.1
| ∑ | ||||||||
M(x,y)= 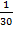 (1•50•160+3•55•170+1•60•165+1•60•170+2•60•175+2•65•170+2•65•175+2•65•180+1•70•165+1•70•170+2•70•175+3•70•180+1•70•185+1•75•175+2•75•180+1•75•190+1•80•175+1•80•185+1•85•185+1•90•190)=
(1•50•160+3•55•170+1•60•165+1•60•170+2•60•175+2•65•170+2•65•175+2•65•180+1•70•165+1•70•170+2•70•175+3•70•180+1•70•185+1•75•175+2•75•180+1•75•190+1•80•175+1•80•185+1•85•185+1•90•190)=  (8000+28050+9900+10200+21000+22100+22750+19800+11550+11900+24500+37800+12950+13125+27000+14250+14000+14800+15725+17100)=
(8000+28050+9900+10200+21000+22100+22750+19800+11550+11900+24500+37800+12950+13125+27000+14250+14000+14800+15725+17100)= 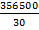 =11883,3333
=11883,3333
cov(x,y)= M(x,y) – M(x)·M(y)= 11883,3333-174.3335·67,8333=11883,3333-11825,6166=57,7167
Найдем выборочный коэффициент корреляции: 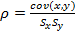
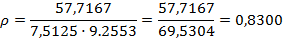
Определим уровень значимости коэффициента корреляции:
Tнаблюдаемое = 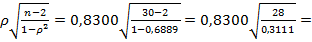
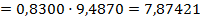
Ткритическое= 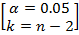
Ткритическое= 
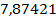 >
>  => Тнаблюдаемое> Ткритическое
=> Тнаблюдаемое> Ткритическое
Вывод: Так как Тнаблюдаемое> Ткритическое, со степенью уверенности 95%, нет основания отвергнуть гипотезу о значимости выборочного коэффициента корреляции.
Часть IV. Уравнения регрессии.
1) Выборочное уравнение линейной регрессии Y на X:
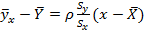
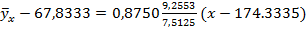

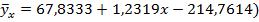
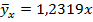 −146,9267
−146,9267
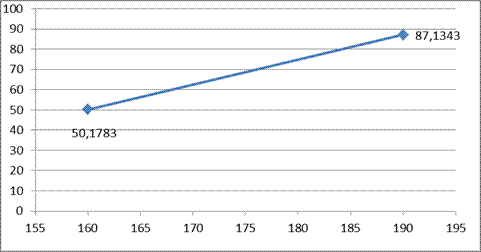
Построим график:
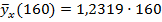 −146,9267=197,104−146,9257=50,1783
−146,9267=197,104−146,9257=50,1783
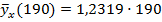 −146,9267=234,061−146,9267=87,1343
−146,9267=234,061−146,9267=87,1343
2) Выборочное уравнение линейной регрессии X на Y:

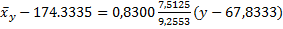
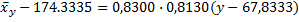

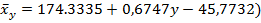
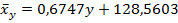
Построим график:
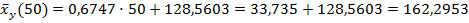
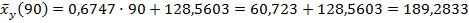

Часть V. Ранговая корреляция.
Таблица 5.1
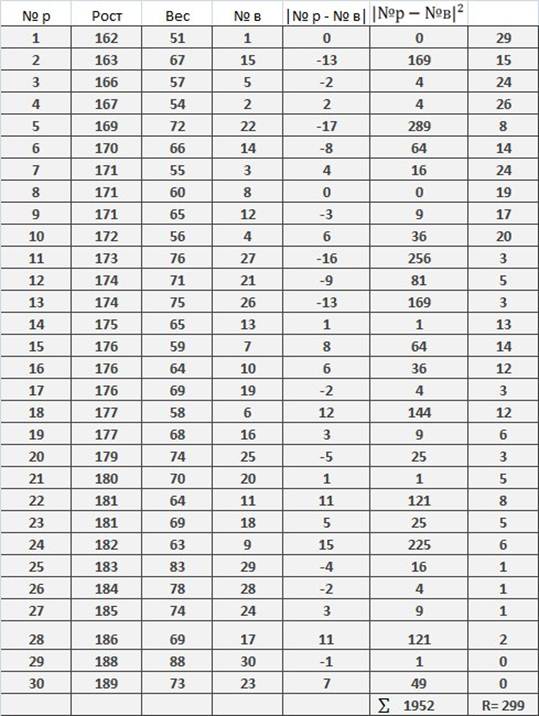
1) Ранговая корреляция Спирмана:
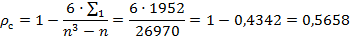
tкритическое= 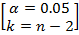
tкритическое= 
Tкритическое=tкритическое· 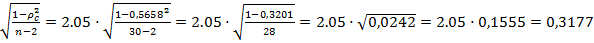
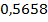 >
> 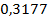 =>
=> 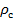 > Tкритическое
> Tкритическое
Вывод: Так как  > Tкритическое , с уверенностью 95% нет основания отвергнуть гипотезу о значимости выборочного коэффициента ранговой корреляции Спирмана.
> Tкритическое , с уверенностью 95% нет основания отвергнуть гипотезу о значимости выборочного коэффициента ранговой корреляции Спирмана.
2) Ранговая корреляция Кендалла:
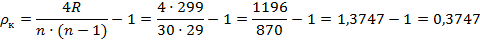
Tкритическое=0,2525
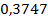 >
> 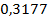 =>
=> 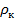 > Tкритическое
> Tкритическое
Вывод: Так как 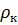 > Tкритическое, с уверенностью 95% нет основания отвергнуть гипотезу о значимости выборочного коэффициента ранговой корреляции Кендалла.
> Tкритическое, с уверенностью 95% нет основания отвергнуть гипотезу о значимости выборочного коэффициента ранговой корреляции Кендалла.
=
Задание 1
Дата добавления: 2015-01-05; просмотров: 255; Мы поможем в написании вашей работы!; Нарушение авторских прав |