
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм пузырьковой сортировки
У нас имеется некоторая последовательность и требуется сделать так, чтобы эти числа стали упорядоченными по возрастанию. Как это делается в алгоритме пузырьковой сортировки. Мы начинаем с самого начала нашей последовательности и сравниваем последовательно два числа. Если правое число меньше левого, то мы меняем эти числа местами. В противном случае мы ничего не делаем.
Сравниваем первые два числа так как правое число больше левого, то мы соответственно ничего не делаем.

Сравниваем следующие два числа: так как 5<8, то мы меняем эти числа местами. Далее сравниваем 3 и 4 позиции: 7<8 -> меняем местами. Сравниваем 4 и 5 позиции 3<8, следовательно их тоже меняем местами.
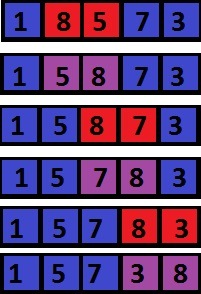
Когда доходим до предпоследней позиции, то мы заканчиваем алгоритм сортировки пузырьком. И теперь начинаем снова с первой позиции, но при этом восьмерку уже не берем в рассмотрении( она уже на своем месте).
Теперь снова сравниваем первые два числа нашей последовательности: 5>1, поэтому ничего не меняем. Следующие два числа тоже оставляем на своих позициях. А вот последние два числа 3 и 7 меняем местами.

Опять уменьшаем количество рассматриваемых чисел нашей последовательности(цифры 7 и 8 уже на своих местах).
Снова начинаем с самого начала и проделываем то же самое.

И вот осталось сравнить два последних числа(3>1), поэтому ничего не делаем.

На этом алгоритм пузырьковой сортировки завершает свою работу — числа нашей последовательности отсортированы в порядке возрастания.
Вот ссылка на видео)) http://www.youtube.com/watch?v=5JMInXAtnQg
4) Сортировка методом вставок.
Сортировка вставками
Сортировка вставками – простой алгоритм сортировки, преимущественно использующийся в учебном программировании. К положительной стороне метода относится простота реализации, а также его эффективность на частично упорядоченных последовательностях, и/или состоящих из небольшого числа элементов. Тем не менее, высокая вычислительная сложность не позволяет рекомендовать алгоритм в повсеместном использовании.
Рассмотрим алгоритм сортировки вставками на примере колоды игральных карт. Процесс их упорядочивания по возрастанию (в колоде карты расположены в случайном порядке) будет следующим. Обратим внимание на вторую карту, если ее значение меньше первой, то меняем эти карты местами, в противном случае карты сохраняют свои позиции, и алгоритм переходит к шагу 2. На 2-ом шаге смотрим на третью карту, здесь возможны четыре случая отношения значений карт:
1. первая и вторая карта меньше третьей;
2. первая и вторая карта больше третьей;
3. первая карта уступает значением третьей, а вторая превосходит ее;
4. первая карта превосходит значением третью карту, а вторая уступает ей.
В первом случае не происходит никаких перестановок. Во втором – вторая карта смещается на место третьей, первая на место второй, а третья карта занимает позицию первой. В предпоследнем случае первая карта остается на своем месте, в то время как вторая и третья меняются местами. Ну и наконец, последний случай требует рокировки лишь первой и третьей карт. Все последующие шаги полностью аналогичны расписанным выше.
Рассмотрим на примере числовой последовательности процесс сортировки методом вставок. Клетка, выделенная темно-серым цветом – активный на данном шаге элемент, ему также соответствует i-ый номер. Светло-серые клетки это те элементы, значения которых сравниваются с i-ым элементом. Все, что закрашено белым – не затрагиваемая на шаге часть последовательности.

C# (с возвратом результата)
public int[] InsertionSort(int[] array){ int[] result = new int[array.Length]; for (int i = 0; i < array.Length; i++) { int j = i; while (j > 0 && result[j - 1] > array[i]) { result[j] = result[j - 1]; j--; } result[j] = array[i]; } return result;}C# (без дополнительной памяти 1)
public void InsertionSort(int[] array){ for (int i = 1; i < array.Length; i++) { int cur = array[i]; int j = i; while (j > 0 && cur < array[j - 1]) { array[j] = array[j - 1]; j--; } array[j] = cur; }}C# (без дополнительной памяти 2)
public void InsertionSort(int[] array){ for (int i = 1; i < array.Length; i++) { int j; int buf = array[i]; for (j = i - 1; j >= 0; j--) { if (array[j] < buf) break; array[j + 1] = array[j]; } array[j + 1] = buf; }}Вот видео для наглядности))) http://www.youtube.com/watch?v=ROalU379l3U
5) Пирамидальная сортировка.
Метод пирамидальной сортировки, изобретенный Д. Уилльямсом, является улучшением традиционных сортировок с помощью дерева.
Пирамидой (кучей) называется двоичное дерево такое, что
a[i] ≤ a[2i+1];
a[i] ≤ a[2i+2].
Подробнее

a[0] — минимальный элемент пирамиды.
Общая идея пирамидальной сортировки заключается в том, что сначала строится пирамида из элементов исходного массива, а затем осуществляется сортировка элементов.
Выполнение алгоритма разбивается на два этапа.
1 этап Построение пирамиды. Определяем правую часть дерева, начиная сn/2-1 (нижний уровень дерева). Берем элемент левее этой части массива и просеиваем его сквозь пирамиду по пути, где находятся меньшие его элементы, которые одновременно поднимаются вверх; из двух возможных путей выбираете путь через меньший элемент.
Например, массив для сортировки
24, 31, 15, 20, 52, 6
Расположим элементы в виде исходной пирамиды; номер элемента правой части (6/2-1)=2 - это элемент 15.

Результат просеивания элемента 15 через пирамиду.
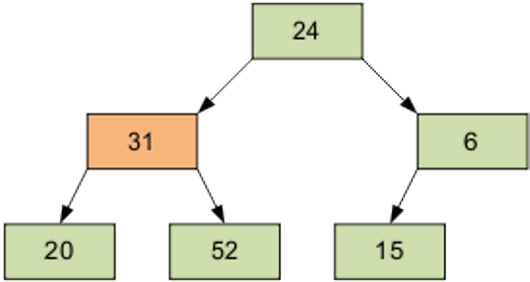
Следующий просеиваемый элемент – 1, равный 31.

Затем – элемент 0, равный 24.

Разумеется, полученный массив еще не упорядочен. Однако процедура просеивания является основой для пирамидальной сортировки. В итоге просеивания наименьший элемент оказывается на вершине пирамиды.
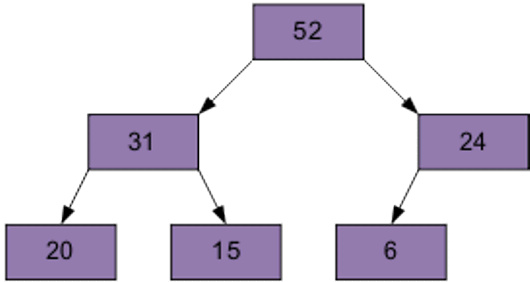
2 этап Сортировка на построенной пирамиде. Берем последний элемент массива в качестве текущего. Меняем верхний (наименьший) элемент массива и текущий местами. Текущий элемент (он теперь верхний) просеиваем сквозь n-1 элементную пирамиду. Затем берем предпоследний элемент и т.д.


Продолжим процесс. В итоге массив будет отсортирован по убыванию.







C#[править]
static Int32 add2pyramid(Int32[] arr, Int32 i, Int32 N) { Int32 imax; Int32 buf; if ((2 * i + 2) < N) { if (arr[2 * i + 1] < arr[2 * i + 2]) imax = 2 * i + 2; else imax = 2 * i + 1; } else imax = 2 * i + 1; if (imax >= N) return i; if (arr[i] < arr[imax]) { buf = arr[i]; arr[i] = arr[imax]; arr[imax] = buf; if (imax < N / 2) i = imax; } return i; } static void Pyramid_Sort(Int32[] arr, Int32 len) { //step 1: building the pyramid for (Int32 i = len / 2 - 1; i >= 0; --i) { long prev_i = i; i = add2pyramid(arr, i, len); if (prev_i != i) ++i; } //step 2: sorting Int32 buf; for (Int32 k = len - 1; k > 0; --k) { buf = arr[0]; arr[0] = arr[k]; arr[k] = buf; Int32 i = 0, prev_i = -1; while (i != prev_i) { prev_i = i; i = add2pyramid(arr, i, k); } } } static void Main(string[] args) { Int32[] arr = new Int32[100]; //заполняем массив случайными числами Random rd = new Random(); for(Int32 i = 0; i < arr.Length; ++i) { arr[i] = rd.Next(1, 101); } System.Console.WriteLine("The array before sorting:"); foreach (Int32 x in arr) { System.Console.Write(x + " "); } //сортировка Pyramid_Sort(arr, arr.Length); System.Console.WriteLine("\n\nThe array after sorting:"); foreach (Int32 x in arr) { System.Console.Write(x + " "); } System.Console.WriteLine("\n\nPress the <Enter> key"); System.Console.ReadLine(); }C# (другой вариант)[править]
public class Heap<T>{ private T[] _array; //массив сортируемых элементов private int heapsize;//число необработанных элементов private IComparer<T> _comparer; public Heap(T[] a, IComparer<T> comparer){ _array = a; heapsize = a.Length; _comparer = comparer; } public void HeapSort(){ build_max_heap();//Построение пирамиды for(int i = _array.Length - 1; i > 0; i--){ T temp = _array[0];//Переместим текущий максимальный элемент из нулевой позиции в хвост массива _array[0] = _array[i]; _array[i] = temp; heapsize--;//Уменьшим число необработанных элементов max_heapify(0);//Восстановление свойства пирамиды } } private int parent (int i) { return (i-1)/2; }//Индекс родительского узла private int left (int i) { return 2*i+1; }//Индекс левого потомка private int right (int i) { return 2*i+2; }//Индекс правого потомка //Метод переупорядочивает элементы пирамиды при условии, //что элемент с индексом i меньше хотя бы одного из своих потомков, нарушая тем самым свойство невозрастающей пирамиды private void max_heapify(int i){ int l = left(i); int r = right(i); int lagest = i; if (l<heapsize && _comparer.Compare(_array[l], _array[i])>0) lagest = l; if (r<heapsize && _comparer.Compare(_array[r], _array[lagest])>0) lagest = r; if (lagest != i) { T temp = _array[i]; _array[i] = _array[lagest]; _array[lagest] = temp; max_heapify(lagest); } } //метод строит невозрастающую пирамиду private void build_max_heap(){ int i = (_array.Length-1)/2; while(i>=0){ max_heapify(i); i--; } } } public class IntComparer : IComparer<int>{ public int Compare(int x, int y) {return x-y;}} public static void Main (string[] args){ int[] arr = Console.ReadLine().Split(' ').Select(s=>int.Parse(s)).ToArray();//вводим элементы массива через пробел IntComparer myComparer = new IntComparer();//Класс, реализующий сравнение Heap<int> heap = new Heap<int>(arr, myComparer); heap.HeapSort();}Дата добавления: 2015-01-05; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |