
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Править]Сравнение сортировок
Рассмотрим массив  . Для элементов должно выполняться отношение порядка.
. Для элементов должно выполняться отношение порядка.
| Название | Лучшее время | Среднее | Худшее | Память | Устойчивость | Обмены (в среднем) | Описание |
| Сортировка пузырьком (Bubble Sort) | 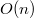
| 
| 
| 
| Да | 
| Алгоритм состоит в повторяющихся проходах по сортируемому массиву. На каждой итерации последовательно сравниваются соседние элементы, и, если порядок в паре неверный, то элементы меняют местами. |
| Сортировка вставками (Insertion Sort) | 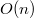
| 
| 
| 
| Да | 
| На каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированной части массива до тех пор, пока весь набор входных данных не будет отсортирован. |
| Сортировка выбором (Selection Sort) | 
| 
| 
| 
| Нет | 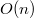
| На  -ом шаге алгоритма находим минимальный среди последних -ом шаге алгоритма находим минимальный среди последних 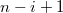 , и меняем его местами с , и меняем его местами с  -ым элементом в массиве. -ым элементом в массиве.
|
| Быстрая сортировка (Quick Sort) | 
| 
|  (маловероятно) (маловероятно)
| 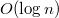 (стек вызовов) (стек вызовов)
| Нет | 
| Один из самых известных и широко используемых алгоритмов сортировки. Алгоритм состоит в выборе опорного элемента, разделении массива на 2 части относительно опорного (одна — все элементы, меньшие опорного элемента, вторая — большие), и в сортировке полученных частей рекурсивным вызовом себя от них. |
| Сортировка слиянием (Merge Sort) | 
| 
| 
| 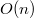 (обычная реализация) (обычная реализация) 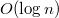 (модифицированная реализация) (модифицированная реализация)
| Да | 
| Алгоритм состоит в разделении массива пополам, сортировки половин и их слиянии. |
| Сортировка кучей (Heap Sort) | 
| 
| 
| 
| Нет | 
| Строим из массива кучу, по очереди извлекаем минимум кучи. |
| Сортировка с помощью бинарного дерева (Tree Sort) | 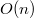
| 
| 
| 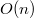
| Да | 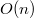
| Добавляем по очереди вершины в сбалансированное дерево поиска, проходим по всем вершинам в порядке возрастания. |
| Карманная сортировка (Bucket Sort) | 
| 
| 
| 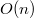
| Да | - | Распределяем элементы в  карманов, сортируем элементы внутри карманов, из каждого кармана данные записываются в массив в порядке разбиения. карманов, сортируем элементы внутри карманов, из каждого кармана данные записываются в массив в порядке разбиения.
|
| Цифровая сортировка (Radix Sort) | 
| 
| 
| 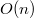
| Да | - | Сортировка объектов равной длины, имеющих "разряды". обычно это строки или целые числа. Алгоритм состоит в том, чтобы отсортировать объекты по разрядам, начиная от младших к старшим. |
| Сортировка подсчетом (Counting Sort) | 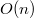
| 
| 
| 
| Да | 
| Сортировка целых чисел, входящих в какой-то небольшой диапазон. Создаем массив длины диапазона  , каждый элемент которого будет показывать, сколько исходных элементов равны данному. Бежим по массиву и считаем количество вхождений каждого числа. , каждый элемент которого будет показывать, сколько исходных элементов равны данному. Бежим по массиву и считаем количество вхождений каждого числа.
|
| Сортировка Хэна (Han's Sort) | 
| 
| 
| 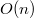
| Да | 
| Очень сложная сортировка, основанная на принадлежности ключей к целым числам. использует экспоненциальное поисковое дерево Андерсона. |
2) Параметры оценки алгоритмов сортировки. Основные этапы работы большинства сортирующих алгоритмов.
Существует много различных алгоритмов сортировки. Все они имеют свои положительные стороны, но общие критерии оценки алгоритма сортировки таковы:
- Насколько быстро данный алгоритм сортирует информацию в среднем?
- Насколько быстро он работает в лучшем и худшем случаях?
- Естественно или неестественно он себя ведет?
- Переставляет ли он элементы с одинаковыми ключами?[1]
Давайте подробнее рассмотрим эти критерии. Очевидно, что скорость работы любого алгоритма сортировки имеет большое значение. Скорость сортировки[2] массива непосредственно связана с количеством сравнений и количеством обменов, происходящих во время сортировки, причем обмены занимают больше времени. Сравнение происходит тогда, когда один элемент массива сравнивается с другим;обмен происходит тогда, когда два элемента меняются местами. Время работы одних алгоритмов сортировки растет экспоненциально, а время работы других логарифмически зависит от количества элементов.
Время работы в лучшем и худшем случаях имеет значение, если одна из этих ситуаций будет встречаться довольно часто. Алгоритм сортировки зачастую имеет хорошее среднее время выполнения, но в худшем случае он работает очень медленно.
Поведение алгоритма сортировки называется естественным, если время сортировки минимально для уже упорядоченного списка элементов, увеличивается по мере возрастания степени неупорядоченности списка и максимально, когда элементы списка расположены в обратном порядке. Объем работы алгоритма оценивается количеством производимых сравнений и обменов.
Чтобы понять, почему переупорядочивание элементов с одинаковыми ключами имеет определенное значение, представьте себе базу данных почтовой рассылки, упорядоченную по главному ключу и подключу. Главным ключом является почтовый индекс, а в пределах одного почтового индекса записи упорядочены по фамилии. При добавлении в список нового адреса и пересортировке списка порядок подключей (то есть фамилий внутри почтовых индексов) не должен меняться. Для гарантии, что это не произойдет, алгоритм сортировки не должен обменивать ключи с одинаковым значением[3].
Далее будут представлены характерные для каждой группы алгоритмы сортировка с анализом эффективности. После них будут продемонстрированы более совершенные методы сортировки.
3) Сортировка методом пузырька.
Дата добавления: 2015-01-05; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |