МЕТОД ПОДСТАНОВКИ

Правила кваліфікації спеціального рецидиву:

1) встановити, що особа вчинила новий злочин у період вступу в силу вироку за раніше вчинений злочин і до погашення або зняття судимості за нього;

2) кваліфікувати новий (рецидивний) злочин – встановити наявність ознак складу простого злочину, врахувати положення КК про стадії вчинення злочину, форму співучасті та вид співучасника;

3) визначити, що раніше вчинений злочин, за який особа була засуджена, є таким, на який вказує диспозиція статті про рецидивний злочин;

4) остаточно кваліфікувати скоєне з врахуванням наявності спеціального рецидиву.

Правила кваліфікації пенітенціарного рецидиву:

1) встановлення того, що злочин вчинений особою в період відбування покарання за раніше вчинений злочин;

2) підтвердження законності призначення особі покарання, в період відбування якого вона вчинила новий злочин;

3) кваліфікацію нового (рецидивного) злочину з встановлення наявності ознак складу простого злочину, кваліфікуючих та особливо кваліфікуючих ознак, врахування положень КК про стадії вчинення злочину, форму співучасті та вид співучасника.

Список рекомендованих джерел

1. Бажанов М. И. Множественность преступлений по уголовному праву Украины / Национальная юридическая академия Украины им. Ярослава Мудрого, Харьковский центр изучения организо­ванной преступности. - X.: Право. - 2000.

2. Батыргареева B.C. Закрепление института рецидива преступле­ний в угорловном законодательстве различных государств // Государство и право.-Москва. - 2005. - №4.

3. Васецов А. Неоднократность, повторность и совокупность при квалификации хищений // Российская юстиция. - 2001. - № 9.

4. Захаров В. Ф. Новий Кримінальний кодекс України та рецидив злочину // Держава і право / Інститут держави і права ім. В. М. Корецького HAH України. - 2002. - Вип. 15.

5. Зелинский А. Ф. Повторение преступлений как преступная деятельность // Государство и право. - 1995. -№ 12.

6. Караев Т. 3. Повторность преступлений. - М.,1983.

7. Кириленко О. І. Види повторності злочинів у кримінальному праві України // Вісник Запорізького юридичного інституту МВС України. - 2001. - Вип. 4 (17).

8. Кириленко О. І. Соціально-правові ознаки множинності зло­чинів // Теорія та практика застосування чинного кримінального та кримінально-процесуального законодавства в сучасних умовах: Тези доп. наук.-практ. конф.: У 2-х ч. - К.: Національна академія внутрішніх справ України, 2002. —4.1.

9. КозловА. В. Совокупность как разновидность множествености преступлений//Вестник Московского университета МВД России. -2006. - №4.

10. Красницький І. В. Питання призначення покарання за множин­ність злочинів у КК України 2001 р. // Львівський інститут внутрішніх справ / Вісник. - Львів. -2003. - №2(1).

11. Кривошеий П. К. Повторность в советском уголовном праве (теоретические и практические проблеми). - К., 1990.

12. Кривошеий П. К. Практика применения уголовного законо­дательства по делам о продолжаемых преступлениях: Учеб. пособ.-К., 1990.

13. Малков В. П. Множественность преступлений и ее формы по советскому уголовному праву. - Казань, 1982.

14. МацневН. И. Основы квалификации сложных насильственных преступлений по совокупности уголовно-правовых норм и при их конкуренции / Н.И.Мацнев, Р.Д.Шарапов / Известия вузов. Правоведение. - СПб. - 2005. - №4.

15. Огородников Н., Борисенко Е. Актуальные проблемы назначе­ния наказания при множественности преступлений // Уголовное право. -2004. -№3.

16. Панько К. А. Вопросы общей теории рецидива в советском уголовном праве. - Воронеж, 1988.

17. Созанський Т. Кваліфікація ідеальної сукупності злочинів // Вісник Львівського інституту внутрішніх справ. - 2001. -Вип. 2(15).

18. Стрижевська А. Визначення змісту поняття «повторність зло­чинів» //Прокуратура, людина, держава. -К.: Істина, 2004. -№ 5.

19. Шевченко Є. В. До питання про причинний зв'язок в злочинах з похідними наслідками // Вісник Академії правових наук України. - X.: Право, 2001. - № 3 (26).

20. ШкредоваЭ.Г. Неоднократность (повторность) и совокупность преступлений как формы множественности по уголовному законодательству стран СНГ // Государство и право. - Москва. -2006. - №8.

Контрольні запитання

1. Які основні відмінності множинності злочинів від одиничного злочину?

2. Назвіть види повторності.

3. Визначте правила кваліфікації повторності злочинів.

4. Чи можлива повторність неоднорідних злочинів?

5. У якому випадку кваліфікація відбувається за різними части­нами статті без взяття до уваги кваліфікуючої ознаки «повтор­ність»?

6. Яка відмінність повторності однорідних злочинів від реаль­ної сукупності злочинів?

7. У чому полягає відмінність повторності злочинів, пов'язаної із засудженням винного за раніше вчинений ним злочин від реци­диву злочинів?

8. Які є види сукупності злочинів?

9. Визначте правила кваліфікації при сукупності злочинів.

10. Які є види рецидиву злочинів?

11. Визначте правила кваліфікації при рецидивові злочинів.

12. Назвіть види одиничних злочинів.

13. Чим продовжуваний злочин відрізняється від триваючого?

14. Чи може складений злочин утворити сукупність з іншим одиничним злочином?

15. Визначте правила кваліфікації одиничного злочину.

Практичні завдання

1. І. організував озброєну групу в складі п'яти осіб. Протягом півроку вони нападали на інкасаторські машини. Допомагав їм в отриманні інформації про рух автомобілів інспектор ДАІ К. Переховував злочинців Г., який раніше був засуджений за недонесення про пограбування.

Кваліфікуйте дії кожного з учасників злочинної діяльності. Дайте правову оцінку ситуації. Визначте форми співучасті та множинність протиправних дій.

2. Громадянин К. знайшов посвідчення працівника міліції. Як нібито працівник міліції, він, разом з П. та В., увійшов до оселі підприємця Д. і почав вимагати повернути державі начебто вкрадені останнім грошові кошти. Після отримання грошей вони побили Д. (заподіявши тяжкі тілесні ушкодження) та забрали ще й телевізор. Через місяць вони таємно проникли до квартири Д. і викрали коштовності.

Кваліфікуйте дії осіб. Визначте вид множинності злочинів і форму співучасті.

3. Раніше судимий за бандитизм К. разом з І. таємно проникли до кафе. Викравши три пляшки горілки вони пішли в дитячий садок та розпили їх. Через дві години вони знову повернулися до кафе та заволоділи двома пляшками коньяку, печивом і магнітофоном. При виході з приміщення їх спробував затримати член громадського формування з охорони громадського прядку П. Заподіявши останньому середньої тяжкості тілесні ушкодження, злодії втекли.

Дайте правову оцінку ситуації. Визначте форми співучасті та множинність протиправних дій.

4. К., працюючи на мотозаводі, підмовив С. і П. займатися таким «бізнесом»: виносити із заводу різноманітні дефіцитні запчастини та збувати їх на базарі. Для здійснення цього плану вони відкрили фірму (документи оформили на дружину С), почали відраховувати певні суми грошей головному інженерові заводу, працівникові охорони Л., а також оперуповноваженому податкової міліції С. Працюючи так близько року та не сплачуючи до того ж податків, вони своїми діями заподіяли державі збитки на суму 20 тис. грн.

Кваліфікуйте дії кожного з учасників злочинної діяльності. Визначте вид множинності злочинів і форму співучасті.

5. І. підмовив раніше судимого за умисне вбивство знайомого на вбивство своєї дружини. Цей знайомий на отримані гроші залучив до «справи» трьох осіб, які протягом року вчиняли в місті крадіжки з квартир. Ці особи під впливом наркотичного сп'яніння вдерлися до оселі подружжя І. та вбили їх.

Дайте правову оцінку ситуації. Визначте форми співучасті та множинність протиправних дій.

6. Начальник районної податкової адміністрації С. разом з оперуповноваженим податкової міліції Я. та податковим інспектором Л. протягом двох років за певну винагороду допомагали зменшувати суми податкових платежів підприємцям Т. і Р. Підприємець Г., дізнавшись про махінації цих осіб, почав вимагати від С. 1000 американських доларів. Домовившись між собою, С, Я. та Л. доручили раніше судимому за розбій А. вбити Г. При спробі реалізувати злочинну мету за допомогою вибухівки А. заподіяв Г. легкі тілесні ушкодження. Через тиждень він довів свій умисел до кінця, вбивши Г. у лікарні. При цьому було поранено п'ятьох хворих осіб, які перебували в одній палаті з Г.

Кваліфікуйте дії кожного з учасників злочинної діяльності. Визначте вид множинності злочинів і форму співучасті.

7. Л. незаконно зберігав пістолет ТТ. Одного разу коли він чистив його, зламав бойову пружину, внаслідок чого зброя перестала бути придатною до стрільби. Через рік Л. придбав бойову пружину та полагодив ТТ.

Чи наявна в діях Л. множинність злочинів?

МЕТОД ПОДСТАНОВКИ

Метод подстановки используется, если из ограничения g(x ,y) = b можно в явном виде выразить функцию y = h(x) . Тогда, подстановка функции y = h(x) в целевую функцию z = f (x , y) вместо переменой y приводит к получению целевой функции вида z = f [x, h(x)] , которая зависит только от одной переменной x. В этом случае задача на условный экстремум функции двух переменных сводится к задаче на безусловный экстремум функции одной переменной.

К основным понятиям, используемым при решении задачи на безусловный экстремум функции одной переменной относятся: точка максимума, точка минимума, точки экстремума, максимум функции, минимум функции, экстремум функции, необходимое условие экстремума функции, критическая точка, достаточное условие экстремума функции.

Точка называется точкой максимума функции f (x) , если в некоторой окрестности точки выполняется неравенство .

Точка называется точкой минимума функции f (x) , если в некоторой окрестности точки выполняется неравенство .

Точки экстремума – общее название точек максимума и минимума функции.

Максимум функции – значение функции в точке ее максимума.

Минимум функции – значение функции в точке ее минимума.

Экстремум функции – общее название максимума и минимума функции.

Необходимое условие экстремума функции одной переменной – равенство нулю ее первой производной (f '(x) = 0).

Критическая точка – точка, в которой выполнено необходимое условие экстремума функции.

Достаточное условие экстремума функции одной переменной: если первая производная дважды дифференцируемой функции равна нулю в некоторой точке , а вторая производная в этой точке положительна, то точка является точкой минимума функции ; если отрицательна, то точка является точкой максимума функции ; если , то вопрос о наличии экстремума в точке остается открытым.

Алгоритм решения задачи на безусловный экстремум функции одной переменной включает следующие этапы.

1. Нахождение производной функции .

2. Нахождение критических точек функции путем приравнивания ее

производной к нулю ( 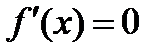) в соответствии с необходимым условием экстремума

функции.

3. Нахождение второй производной функции и проверка достаточного условия экстремума функции в каждой критической точке.

4. Вычисление локальных экстремумов функции.

5. Нахождение глобальных максимума и минимума функции (при наличии нескольких максимумов или минимумов). Глобальный максимум функции определяется как наибольший локальный максимум. Глобальный минимум функции определяется как наименьший локальный минимум.

Алгоритм решения задачи на безусловный экстремум функции двух переменныхz = f ( x , y ) включает следующие этапы.

1. Нахождение частных производных функции z = f (x , y) и приравнивание их к нулю в соответствии с необходимым условием безусловного экстремума функции. В результате получится система из двух уравнений вида

Частной производной первого порядка (первой частной производной или просто частной производной) функции двух переменных z = f (x , y) по переменной x называется производная данной функции, вычисленная при фиксированном значении переменной y как обыкновенная производная функции одной переменной x . Она обозначается как

Частной производной первого порядка функции двух переменных z = f (x , y) по переменной y называется производная данной функции, вычисленная при фиксированном значении переменной x как обыкновенная производная функции одной переменной y . Она обозначается как .

Функция, имеющая частные производные первого порядка, называется дифференцируемой.

Теорема (необходимое условие экстремума функции двух переменных): если в точке максимума или минимума все частные производные существуют и непрерывны, то они равны нулю в этой точке.

2. Нахождение критических точек, в которых целевая функция задачи z = f (x , y) может иметь экстремум путем решения полученной системы уравнений.

Критическими (или стационарными) точками называются точки, в которых выполнено необходимое условие экстремума функции (равенство нулю всех частных производных).

3. Нахождение частных производных второго порядка функции z = f (x , y) , вычисление их значений в каждой критической точке и проверка достаточного условия безусловного экстремума функции двух переменных в каждой критической точке.

Частной производной второго порядка (второй частной производной)функции z = f (x , y) называется частная производная первого порядка от частной производной первого порядка данной функции. Функция двух переменных вида z = f (x , y) имеет четыре частных производных второго порядка:

Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называются смешанными производными.

Частные производные более высоких порядков определяются аналогичным образом.

Теорема. Если функция z = f (x , y) дважды дифференцируема в точке , то ее смешанные производные в этой точке равны, то есть

Поэтому величина смешанной производной функции двух переменных не зависит от порядка переменных, по которым берутся производные.

Теорема (достаточное условие экстремума функции двух переменных). Если функция z = f (x , y):

а) определена в некоторой окрестности критической точки , в которой обе частные производные равны нулю

б) имеет в этой точке непрерывные частные производные второго порядка, равные

то характер этой точки определяется значением величины .

Если , то в точке функция z = f (x , y) имеет экстремум (максимум при A < 0 и минимум при A > 0 ).

Если , то в точке функция z = f (x , y) не имеет экстремума.

Если , то вопрос о наличии экстремума в точке функции z = f (x , y) остается открытым.

Данная теорема применима для проверки достаточного условия экстремума функции только двух переменных.

В общем случае для проверки достаточного условия экстремума функции нескольких переменных используется следующая теорема.

Теорема (достаточное условие экстремума функцииn переменных).Если точка является критической точкой функции n переменных , и в окрестности этой точки существуют и непрерывны частные производные второго порядка, тогда

1) если матрица Гессе положительно определена в точке , то данная точка является точкой минимума функции z;

2) если матрица Гессе отрицательно определена в точке , то данная точка является точкой максимума функции z ;

3) если матрица Гессе не является знакоопределенной в точке , то функция z в данной точке не имеет экстремума.

Матрицей Гессеназывается матрица, элементами которой являются частные производные второго порядка функции по всем переменным , вида

Определитель матрицы Гессе называется гессианом.