МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА

Метод множителей Лагранжаиспользуется, если из ограничения невозможно в явном виде выразить функцию (то есть невозможно использовать метод подстановки). Метод множителей Лагранжа, также как и метод подстановки, позволяет перейти от задачи на нахождение условного экстремума функции к задаче на нахождение безусловного экстремума функции.

Алгоритм решения задачи на условный экстремум целевой функции двух переменных с одним ограничением методом множителей Лагранжавключает следующие этапы.

1. Введение вспомогательной переменной l , называемой множителем Лагранжа, и составление функции Лагранжа, которая представляет собой сумму целевой функции и ограничения, умноженного на множитель Лагранжа, вида

Метод множителей Лагранжа основан на том, что точка условного экстремума 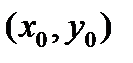функции при условии совпадает с точкой безусловного экстремума функции Лагранжа.

2. Нахождение частных производных функции Лагранжа по переменным и приравнивание их к нулю в соответствии с необходимым условием безусловного экстремума функции. В результате получится система из трех уравнений вида

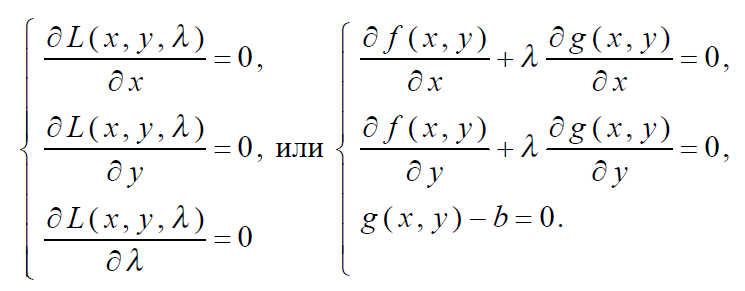
3. Нахождение критических (стационарных) точек, в которых функция Лагранжа (и соответственно целевая функция исходной задачи ) может иметь экстремум путем решения полученной системы уравнений.

4. Проверка достаточного условия экстремума функции Лагранжа с использованием достаточного условия экстремума функции двух переменных (так как функция Лагранжа при конкретном значении множителя Лагранжа 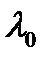становится функцией двух переменных) или достаточного условия экстремума функции n переменных при n > 2 (путем установления знакоопределенности матрицы Гессе, составленной из частных производных второго порядка функции Лагранжа по переменным x и y, на основе критерия Сильвестра).

5. Вычисление локальных экстремумов функции и выбор того из них, в котором целевая функция задачи принимает максимальное (минимальное) значение.

В общем случае при решении задач нелинейного программирования вида

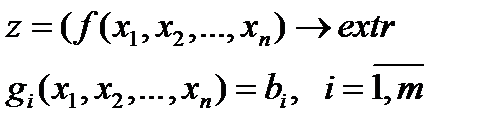
функция Лагранжа определяется выражением

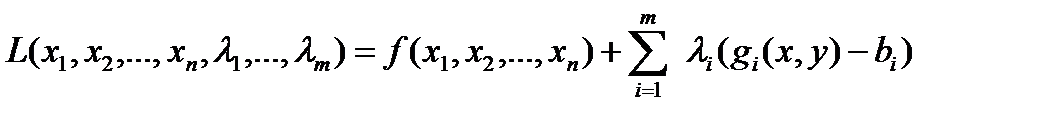
Система из (n + m) уравнений для нахождения критических точек имеет вид

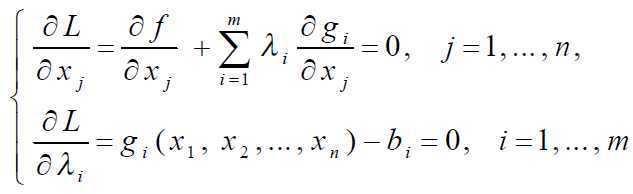
Для проверки достаточного условия экстремума функции Лагранжа составляется матрица Гессе порядка n из частных производных второго порядка по переменным .

Множители Лагранжа, соответствующие экстремальному значению целевой функции, характеризуют чувствительность экстремального значения целевой функции к изменениям констант ограничений . Они равны

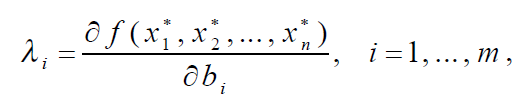
и показывают, как изменится экстремальное значение целевой функции при изменении значения константы в i -м ограничении на 1 единицу.

Например, если какой-то множитель Лагранжа равен нулю, то малые изменения соответствующей константы ограничений не окажут никакого влияния на экстремальное значение целевой функции.

В экономических задачах распределения ресурсов целевая функция имеет размерность стоимости, то есть цены, умноженной на объем продукции (например, прибыль, выручка, издержки), а с помощью ограничений устанавливается определенное значение некоторого количества (например, затрат). В таких задачах с помощью множителя Лагранжа определяется чувствительность целевой функции, имеющей размерность стоимости, к изменениям некоторого количества. Поэтому множитель Лагранжа имеет размерность цены и характеризует ценность какого-либо i -о ресурса. Поэтому множитель Лагранжа также называется теневой ценой (данного вида затрат).

Пример

Имеется два способа производства некоторого продукта. Издержки производства при каждом способе зависят от произведенных y₁ и у₂ следующим образом: g(x₁)=9x₁ + x₁², g(x₂)=6x₂ + x₂² . За месяц необходимо произвести 150 единиц продукции, распределив ее между двумя способами так, чтобы минимизировать общие издержки.

Решение
Найдем экстремум функции F(X) = 9x₁+x₁²+6x₂+x₂², используя функцию Лагранжа:

где
- целевая функция вектора .
- ограничения в неявном виде.
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция:
F(X) = 9x₁+x₁²+6x₂+x₂²
Перепишем ограничение задачи в неявном виде:

Составим вспомогательную функцию Лагранжа:

Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным х_i и неопределенному множителю λ.
Составим систему:
∂L/∂x₁ = 2x₁+λ+9 = 0
∂L/∂x₂ = λ+2x₂+6 = 0
∂F/∂λ = x₁+x₂ -150= 0
Систему решаем с помощью метода Гаусса или используя формулы Крамера.

Запишем систему в виде:

Для удобства вычислений поменяем строки местами:

Добавим 2-ую строку к 1-ой:

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

Из 1-ой строки выражаем x₃

Из 2-ой строки выражаем x₂

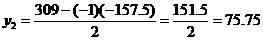
Из 3-ой строки выражаем x₁

Таким образом, чтобы общие издержки производства были минимальны, необходимо производить x₁ = 74.25; x₂ = 75.75.