Порядок выполнения лабораторной работы.

1) Выкрутить цилиндры 8 из диска 1.

2) К свободному концу нити подвесить груз массой .

3) При полностью размотанной со шкива нити линейкой измерить высоту от столика установки 5 до груза 3.

4) Включить секундомер в сеть.

5) Включить включатель секундомера на задней панели, при этом секундомер должен показывать «00.0», а измеритель перемещения «0.00».

6) Вращая диск и наматывая нить на шкив с левой стороны, поднять груз на выбранную высоту над столиком установки и, нажав кнопку электромагнита, зафиксировать груз в этом положении.

7) Измерить высоту линейкой и найти высоту падения

8) Нажать кнопку секундомера «пуск» и дождаться, пока секундомер перестанет считать время, а измеритель перемещения перестанет считать высоту подъема груза.

9) Показание секундомера – время падения груза и показание измерителя перемещения – высоту подъема записать в табл. 3.1.1.

10) Выключить включатель секундомера.

11) Повторить еще два раза измерения и при падении груза с той же высоты .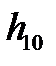

12) Измерить три раза время падения и высоту подъема при падении груза с той же высоты , когда нить намотана на шкив с правой стороны.

13) Выключить секундомер.

Таблица 3.1.1

							Среднее значение
, с
, м

=__________ = __________ = _________

2.3. Задания к упражнению 1

(результаты вычислений внести в таблицу 3.1.2)

1) Вычислить высоту падения груза .

2) Вычислить средние значения времени падения и высоты подъема груза :

3) Учитывая, что падение груза и вращение диска равноускоренные, выразить через измеренные и заданные величины , , 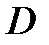и вычислить:

а) ускорение падения груза , используя формулу пути;

б) скорость груза в конце падения (в начале торможения) , используя формулу скорости;

в) угловую скорость диска в конце падения груза, принимая, что нить намотана плотно и проскальзывание нити по шкиву отсутствует и линейная скорость точек обода шкива равна скорости груза , и используя связь линейной скорости с угловой;

г) угловое ускорение диска 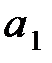, предполагая, что проскальзывание нити по шкиву и растяжение нити отсутствуют и тангенциальное ускорение точек обода шкива равно ускорению падения груза 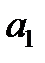, и используя связь с .

д) угол поворота диска за время падения груза ;

е) число оборотов диска во время падения груза, учитывая, что одному обороту соответствует угол поворота .

4) Пренебрегая массой нити и действующими на груз силой сопротивления воздуха и силой Архимеда, получить через измеренные и заданные величины , , , и вычислить:

а) силу натяжения нити при падении груза, пользуясь формулой 2-го закона Ньютона;

б) момент силы натяжения , действующий на диск при падении груза, пользуясь формулой определения момента силы.

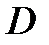5) Пренебрегая потерей механической энергии при изменении направления движения груза и принимая, что груз начинает подниматься со скоростью , равной скорости падения груза , выразить через измеренные и заданные величины , , , , и вычислить:

а) ускорение при подъеме груза, используя выражение разности квадратов скоростей через ускорение и пройденный путь;

б) время подъема груза , используя формулу скорости;

в) угловую скорость диска в начале подъема груза, учитывая, что и используя связь с ;

г) угловое ускорение диска при подъеме груза, используя связь с ;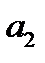

д) угол поворота диска за время подъема груза , используя выражение разности квадратов угловых скоростей через угловое ускорение и угол поворота;

е) число оборотов диска во время подъема груза;

ж) силу натяжения нити при подъеме груза, используя формулу 2-го закона Ньютона;

з) момент силы натяжения при подъеме груза, используя формулу определения момента силы.

6) Принимая моменты сил сопротивления движению диска при падении груза и подъеме груза одинаковыми и равными и применяя основной закон динамики вращательного движения для диска при падении груза и при подъеме груза, и используя

выражения угловых ускорений и 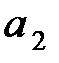и моментов сил и , полученных в заданиях 3.г, 5.г, 4.б, 5.з, получить:

а) выражения для момента сил сопротивления

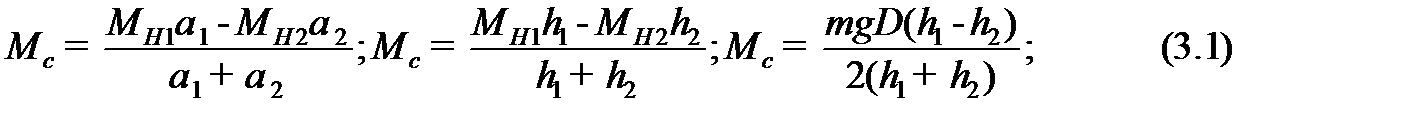
б) выражения для момента инерции диска

7) Подставив значения измеренных величин , , и заданных величин ,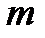

, вычислить:

а) момент сил сопротивления ;

б) момент инерции диска .

8) Принимая за нулевой уровень потенциальной энергии груза высоту , а потенциальную энергию диска постоянной и равной 0 Дж, и используя формулу потенциальной энергии взаимодействия груза с Землей, формулы кинетической энергии поступательного и вращательного движения тел и определение механической энергии тела и системы, получить выражения через величины , , , , , 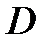механической энергии:

а) груза в начале падения ;

б) диска в начале падения ;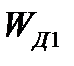

в) системы тел, состоящей из груза и диска, в начале падения ;

г) груза в конце падения ;

д) диска в конце падения ;

е) системы тел, состоящей из груза и диска, в конце падения :

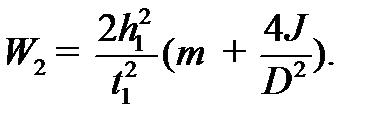
9) Получить выражение потери механической энергии системы при падении груза через , , , , :

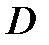10) Пренебрегая потерей механической энергии при изменении направления движения груза, принять, что механическая энергия системы в начале подъема груза равна энергии системы в конце падения .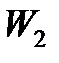

11) Получить выражение через и m механической энергии системы 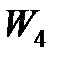в конце подъема груза.

12) Получить выражение потери механической энергии системы при подъеме груза через , , , , :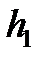

13) Принимая моменты сил сопротивления движению диска при падении груза и подъеме груза одинаковыми и равными , и используя формулу работы момента силы, получить выражения работы момента сил сопротивления:

а) при падении груза

б) при подъеме груза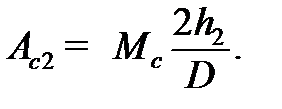

14) Учитывая неконсервативные силы, действующие только на диск, работы момента сил сопротивления и выразить через потери механической энергии и .

15) Приравняв выражения работ момента сил сопротивления при падении груза и подъеме груза через и через и , составить систему двух уравнений с неизвестным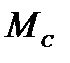и и и получить выражения через , , , , :

а) момента сил сопротивления – выражение (3.1);

б) момента инерции диска - выражение (3.2).

16) Подставив значения измеренных величин , , , заданных величин , и вычисленных в задании 6 величин и , вычислить:

а) механическую энергию груза , диска и системы , состоящей из груза и диска, в начале падения груза;

б) механическую энергию груза , диска и системы в конце падения груза;

в) потерю механической энергии системы при падении груза ;

г) механическую энергию системы в начале подъема и в конце подъема груза ;

д) потерю механической энергии системы при подъеме груза ;

е) работу сил неконсервативных взаимодействий при падении груза = ;

ж) работу сил неконсервативных взаимодействий при подъеме груза = ;

з) потерю механической энергии системы и работу сил неконсервативных взаимодействий в процессе падения и подъема груза

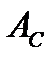= Δ = – .

и) долю потерянной механической энергии системы в процессе падения и

подъема груза ;

к) долю механической энергии системы, потерянной при падении груза

л) долю механической энергии системы, потерянной при подъеме груза ;

17) Вычислить момент инерции диска 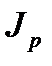, включая моменты инерции прикрепленной к диску пластины 6, шкива 2, цилиндрического вала 7 (рис. 3.2), используя формулы

моментов инерции тел; плотность стали = 7800 кг/м³; на рисунке размеры указаны в сантиметрах; пластину рассматривать как стержень.

18) Сравнить вычисленное по формулам значение момента инерции 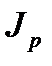с

полученным значением на основе опытных данных; найти значение ;

сделать вывод о правомочности принятых допущений.

Рис. 3.2

Таблица 3.1.2

Номер задания								3,а	3,б	3,в
Величина
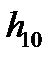
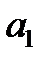
Наименование единицы измерения	м	кг	м	м	м	с	м	м/с2	м/с	с-1
Численное значение

Таблица 3.1.2 (продолжение)

3,г	3,д	3,е	4,а	4,б		5,а	5,б	5,в	5,г	5,д	5,е
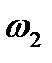
с-2	рад	об	Н	Н . м	м/с	м/с2	с	с-1	с-2	рад	об

Таблица 3.1.2 (продолжение)

5,ж	5,з	7,а	7,б	16,а	16,а	16,а	16,б	16,б	16,б	16,в	16,г
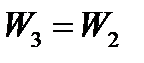
Н	Н	Н . м	кг.м2	Дж	Дж	Дж	Дж	Дж	Дж	Дж	Дж

Таблица 3.1.2 (окончание)

16,г	16,д	16,е	16,ж	16,з	16,и	16,к	16,л
Дж	Дж	Дж	Дж	Дж	%	%	%	кг.м2	%

3.2. Упражнение 2. Исследование зависимости момента инерции тел