Какие методы используют для расчёта цепей с индуктивно связанными элементами?

Ответ: Основой расчета являются уравнения цепи (Кирхгофа, контурные или узловые), составленные с учетом взаимного влияния индуктивно связанных элементов. Для анализа последовательного соединения двух связанных катушек используем уравнения Кирхгофа. При этом маркированные зажимы последовательно включенных катушек могут быть соединены по-разному. Суммарное напряжение согласно включенных катушек (рис. 9.4, а) равно:

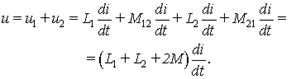
Величина L_э = (L₁ + L₂ + 2M) в этом случае представляет собой - эквивалентную индуктивность.

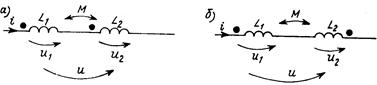
Рис. 9.4

Для встречного включения (рис. 9.4, б) имеем: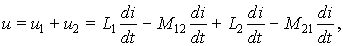

и эквивалентная индуктивность равна L_э = (L₁ + L₂ – 2M).

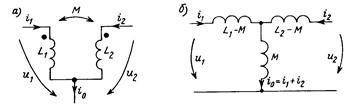
Рис. 9.5

Если две индуктивно связанные катушки (рис. 9.5, а) имеют общую точку (пусть, например, их немаркированные зажимы соединены друг с другом), то, переписав соотношения для напряжений (9.1) в форме:

получаем возможность заменить их Т-образной схемой замещения, не содержащей индуктивных связей (рис. 9.5, б).

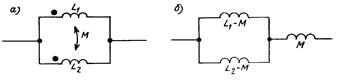
Рис. 9.6

Для определения эквивалентной индуктивности параллельно соединенных катушек (рис. 9.6, а), преобразуем эту схему в изображенную на рис. 9.6, б. Поскольку индуктивности при последовательном и параллельном соединениях суммируются по тем же правилам, что и сопротивления, для эквивалентной индуктивности параллельного соединения имеем:

Так как соединенные произвольным образом катушки сохраняют индуктивный характер, то эквивалентная индуктивность при встречном и параллельном соединениях имеет положительное значение, несмотря на наличие отрицательных слагаемых в полученных выражениях. Это означает, что значения L₁, L₂ и M двух катушек не независимы друг от друга, а связаны неравенствами:L₁L₂  M²; L₁ + L₂ 2M. Возведением второго из неравенств в квадрат можно убедиться, что оно является более сильным, чем первое неравенство, т. е. условие L₁L₂  M² обеспечивает выполнение и второго неравенства. Величина — коэффициент связи обмоток — характеризует степень взаимного влияния обмоток друг на друга. При k = 1 или 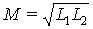имеем совершенную связь обмоток —

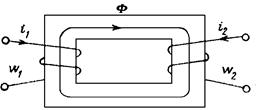Рис. 9.7

весь поток, создаваемый одной обмоткой, пересекает сечение витков второй обмотки. К этому режиму можно приблизиться, помещая обе обмотки на общем сердечнике (рис. 9.7), материал которой имеет высокую магнитную проницаемость, либо располагая их витки бесконечно близко друг к другу. При указанных приближениях получим для индуктивности

первой обмотки L₁=w₁Φ/i₁= 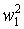/R_м (R_м — магнитное сопротивление сердечника). Аналогично L₂= 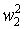/R_м; M=w₁w₂/R_м и k=1. В системе произвольного числа индуктивно связанных обмоток для любой пары выполняется условие 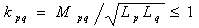и матрица взаимных индуктивностей Мявляется при отсутствии совершенных связей (k_pq< 1) положительно определенной. При сильной связи обмоток (k  1) одна из индуктивностей в Т-образной схеме замещения (рис. 9.5, б) может оказаться отрицательной. Так, при L₁> M > L₂ имеем L₂ – M < 0. Поэтому эквивалентную схему с взаимной индуктивностью (рис. 9.5, а) можно использовать для моделирования цепей с отрицательной индуктивностью. Для расчета разветвленных цепей с индуктивно связанными элементами (рис. 9.8) используем метод контурных токов.

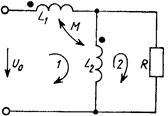
Рис. 9.8

Контурные уравнения в комплексной форме имеют общий вид: 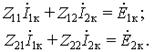Выбор независимых контуров указан стрелками на схеме.

При записи собственных и общих сопротивлений запишем по уже известным правилам сначала члены, не связанные с взаимной индуктивностью. Далее учтем члены, отражающие индуктивные связи. В собственных сопротивлениях контуров слагаемые + j2ωM появляются, если обе индуктивно связанные катушки входят в данный контур и их маркировка соответствует согласному включению в этом контуре. Если при обходе контура, включающего две связанные катушки, одна из катушек обтекается контурным током в положительном, а другая – в отрицательном направлении, то член в соответствующем собственном сопротивлении будет иметь знак “минус”, т. е. – j2ωM. При записи общего сопротивления двух контуров учитывается их взаимное индуктивное влияние друг на друга. Здесь член jωM имеет знак “плюс”, если положительные направления обоих контурных токов ориентированы одинаково относительно маркированных зажимов катушек, и оба тока протекают по ним либо в положительном, либо в отрицательном направлении. Если же один из влияющих друг на друга токов протекает в положительном, а другой – в отрицательном направлении, в общем сопротивлении контуров учитывают член – jωM. С учетом сформулированных правил получим для контурных сопротивлений цепи (см. рис. 9.8):

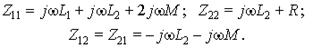
Дата добавления: 2015-01-14; просмотров: 15; Нарушение авторских прав