
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Привести схему замещения и уравнения равновесия напряжений первичной и вторичной цепей воздушного трансформатора.
Ответ: Воздушный трансформатор (рис. 6.14) является классическим примером линейной цепи, имеющей индуктивную связь.

Рис.6.14. Схема линейного трансформатора.
Полные магнитные потоки, создаваемые токами катушек, можно представить как сумму магнитного потока Φ12 или Φ21, сцепленного с витками другой катушки, и потока рассеяния Φs1 или Φs2, т.е. Φ11 = Φ21 + Φs1 и Φ22 = Φ12 + Φs2. Индуктивности катушек:  , 126(6.16)
, 126(6.16)
 , 127(6.17)
, 127(6.17)
где: Ls1, Ls2 индуктивности рассеяния.  , 128(6.18)
, 128(6.18)
 . 129(6.19). Вводится понятие коэффициента трансформации, который представляет собой отношение числа витков первичной обмотки к числу витков вторичной обмотки
. 129(6.19). Вводится понятие коэффициента трансформации, который представляет собой отношение числа витков первичной обмотки к числу витков вторичной обмотки  . С учетом заданных положительных направлений токов и напряжений в обмотках составим уравнения электрического равновесия для трансформатора, выбрав направление обхода в катушках по часовой стрелке.
. С учетом заданных положительных направлений токов и напряжений в обмотках составим уравнения электрического равновесия для трансформатора, выбрав направление обхода в катушках по часовой стрелке.  ;
;
 . 130(6.20)
. 130(6.20)
Преобразуем данные уравнения следующим образом:  ;
; 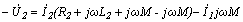 .
.
Перегруппируем слагаемые: 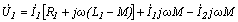 ;
;
 . 131(6.21) Полученная система уравнений позволяет построить схему замещения воздушного трансформатора, представленную на рис. 6.15.
. 131(6.21) Полученная система уравнений позволяет построить схему замещения воздушного трансформатора, представленную на рис. 6.15.

Рис.6.15. Схема замещения линейного трансформатора
Индуктивные элементы (L1 M) и (L2 M) замещают в реальном трансформаторе индуктивности потокорассеяния при условии, что количество витков катушек равны(n = 1).  . Сопротивления R1 и R2 замещают активное сопротивление проводов катушек. Индуктивный элемент М замещает в трансформаторе поток взаимной индукции.
. Сопротивления R1 и R2 замещают активное сопротивление проводов катушек. Индуктивный элемент М замещает в трансформаторе поток взаимной индукции.
В полученной схеме отсутствует магнитная связь между катушками, и теперь они соединены электрически. Однако в подавляющем числе случаев W1 не равно W2 и поэтому прибегают к составлению приведенной схемы замещения трансформатора, для которой параметры вторичной цепи приводятся к первичной. Для реализации такого приведения  умножается на n, а
умножается на n, а  делится на n. Вновь преобразуем исходные уравнения:
делится на n. Вновь преобразуем исходные уравнения: 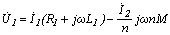 ;
;  . Аналогичного рода преобразования:
. Аналогичного рода преобразования:  ;
;  .
.
Перегруппируем слагаемые:  ;
;
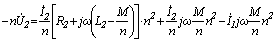 . 132 (6.22)
. 132 (6.22)
На основании системы уравнений (6.22) составим схему замещения трансформатора (рис. 6.16).

Рис.6.16. Схема замещения воздушного трансформатора при
различных количествах витков в катушках: 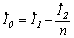 .
.  - носит название намагничивающего тока холостого хода трансформатора. Смысловое содержание параметров схемы замещения остается тем же. Вносимое сопротивление трансформатора. Пусть к выходным зажимам трансформатора по рис. 6.17 подключен приемник с сопротивлением Zн. Zн=Rн+jXн.
- носит название намагничивающего тока холостого хода трансформатора. Смысловое содержание параметров схемы замещения остается тем же. Вносимое сопротивление трансформатора. Пусть к выходным зажимам трансформатора по рис. 6.17 подключен приемник с сопротивлением Zн. Zн=Rн+jXн.
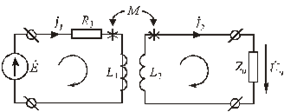
Рис.6.17. Схема нагруженного трансформатора
Вновь составим систему уравнений для данной цепи по законам Кирхгофа с учетом выбранного направления обхода.  133 (6.23)
133 (6.23)
Выразим из второго уравнения ток  и подставим его в первое уравнение. Так как
и подставим его в первое уравнение. Так как  , то получим следующее выражение для тока
, то получим следующее выражение для тока  :
:  . Подставляя его в первое уравнение, получим:
. Подставляя его в первое уравнение, получим:
 ; 134(6.24)
; 134(6.24) 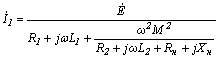 .
.
Проведя ряд алгебраических преобразований, получим следующее выражение для тока  :
: 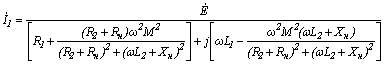 .
.
Обозначим: 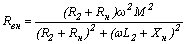 , 135(6.25).
, 135(6.25).  , 136(6.26) ,где: Rвн, и Xвн – соответственно активное и реактивное вносимые сопротивления трансформатора. Тогда окончательно имеем:
, 136(6.26) ,где: Rвн, и Xвн – соответственно активное и реактивное вносимые сопротивления трансформатора. Тогда окончательно имеем:  . 137(6.27). Физически вносимое сопротивление представляет собой такое сопротивление, включенное последовательно с первичной обмоткой, которое позволяет учесть влияние тока нагрузки
. 137(6.27). Физически вносимое сопротивление представляет собой такое сопротивление, включенное последовательно с первичной обмоткой, которое позволяет учесть влияние тока нагрузки  на ток
на ток 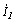 .
.
72)Построить векторную диаграмму токов и напряжений воздушного трансформатора. Объяснить порядок построения.
Ответ: Поскольку первичная и вторичная обмотки трансформатора с параметрами соответственно R1,L1 и R2,L2 представляют собой 2 индуктивно связанные и встречно включенные катушки, уравнения Кирхгофа, составленные для цепей первичной и вторичной обмоток можно записать в следующем виде:
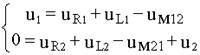 ,
,
где: uR1, uR1- напряжения на активных сопротивлениях первичной и вторичной обмоток трансформатора, uL1, uL2- напряжения на индуктивностях первичной и вторичной обмоток, uм12- напряжение взаимоиндукции в первичной обмотке, обусловленное током вторичной обмотки, uм21- напряжение взаимоиндукции во вторичной обмотке, обусловленное током первичной обмотки, u2- напряжение на нагрузке. Поскольку ток во вторичной обмотке обусловлен напряжением взаимоиндукции uм21, то это слагаемое во втором уравнении целесообразно перенести в левую часть и записать систему в виде:
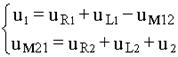 . (8.1)
. (8.1)
Если напряжение на первичной обмотке трансформатора синусои-дально, то систему (8.1) можно записать в комплексной форме:
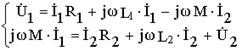 (8.2)
(8.2)
Графической интерпретацией системы (8.2) является векторная диаг-рамма воздушного трансформатора, представленная на рис. 8.2.

При построении диаграммы считаются заданными векторы тока и напряжения на нагрузке 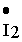 ,
,  . Данная диаграмма соответствует активно-индуктивной нагрузке. Диаграмма строится в следующем порядке:
. Данная диаграмма соответствует активно-индуктивной нагрузке. Диаграмма строится в следующем порядке:
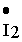





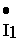

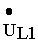

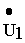
Дата добавления: 2015-01-14; просмотров: 360; Мы поможем в написании вашей работы!; Нарушение авторских прав |