
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Что представляет дискретный ряд Фурье? Привести 2 формы записи дискретного ряда Фурье.
Ответ: Известно, что периодическая с периодом  ограниченная кусочно-гладкая функция
ограниченная кусочно-гладкая функция  может быть представлена своим рядом Фурье:
может быть представлена своим рядом Фурье:
 ,
,
где:  . Преобразование Фурье: Для непериодических функций ряд Фурье заменяется интегралом Фурье:
. Преобразование Фурье: Для непериодических функций ряд Фурье заменяется интегралом Фурье:
 где:
где:  .
.
Связь между рядом Фурье и преобразованием Фурье: Рассмотрим функцию  , равную нулю вне интервала
, равную нулю вне интервала  . С одной стороны, для нее можно определить преобразование Фурье, а с другой стороны, ее можно считать периодически продолженной и определить для нее коэффициенты ряда Фурье. Тогда имеем:
. С одной стороны, для нее можно определить преобразование Фурье, а с другой стороны, ее можно считать периодически продолженной и определить для нее коэффициенты ряда Фурье. Тогда имеем:  Сравнивая полученные выражения, можно сделать вывод, что:
Сравнивая полученные выражения, можно сделать вывод, что: 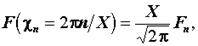 т.е. коэффициенты ряда Фурье для периодического продолжения функции
т.е. коэффициенты ряда Фурье для периодического продолжения функции  определяют значение преобразования Фурье в дискретных точках
определяют значение преобразования Фурье в дискретных точках  . Дискретное преобразование Фурье: Для последовательности
. Дискретное преобразование Фурье: Для последовательности 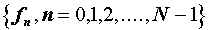 , состоящей из
, состоящей из  действительных или комплексных чисел определяется дискретное преобразование Фурье (ДПФ)
действительных или комплексных чисел определяется дискретное преобразование Фурье (ДПФ)  :
:
 ,
,
где:  — дискретные экспоненциальные функции.
— дискретные экспоненциальные функции.
Так как дискретные экспоненциальные функции  являются ортогональными, т.е. удовлетворяют условию:
являются ортогональными, т.е. удовлетворяют условию: 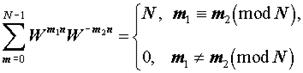 то справедливо обратное дискретное преобразование Фурье (ОДПФ):
то справедливо обратное дискретное преобразование Фурье (ОДПФ): 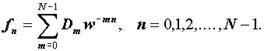
Дата добавления: 2015-01-14; просмотров: 381; Мы поможем в написании вашей работы!; Нарушение авторских прав |