Закон сохранения импульса механической системы.

В замкнутой системе импульс сохраняется.

Другая формулировка: Суммарный импульс замкнутой системы остается постоянным по модулю и направлению, хотя импульс каждого из тел системы может изменяться.

Доказательство:

Рассмотрим механическую систему из N тел, массы и скорости которых соответсвенно равны m1, m2, ..., mN; V1, V2, ..., VN.

Запишем второй закон Ньютона для каждого из N тел механической системы:

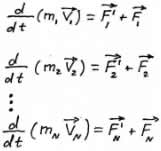
где Fi - равнодействующая внутренних сил i-того тела системы, F - равнодействующая внешних сил i-того тела системы.

Проведем почленное сложение уравнений:

(1)

Рассмотрим левую часть полученного выражения.

= =

где = представляет собой суммарный импульс всех тел системы, т.е. импульс системы.

Первый член в правой части выражения (1) представляет собой векторную сумму внутренних сил всех тел системы. По третьему закону Ньютона каждой внутренней силе F'mn соответствует равная ей по модулю и противоположная по направлению сила F'nm, поэтому:

=0.

Выражение преобразуется к виду:

=

Производная от импульса системы по времени равна сумме внешних сил, действующих на систему.

Если сумма (векторная) внешних сил равна нулю, или внешние силы отсутствуют, то:

, т.е. импульс сохраняется.

Дополнение:

Импульсом (или количеством движения) материальной точки (тела) называется векторная величина, численно равная произведению массы материальной точки (тела) на ее скорость и меющая направление скорости: p = mV (единица импульса - 1 (кг*м/с)).