Вид преобразований при коллинеарных осях

Если ИСО S' движется относительно ИСО S с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

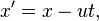
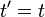или, используя векторные обозначения,

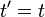
(последняя формула остается верной для любого направления осей координат).

Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей (много меньше скорости света).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета.

Механический принцип относительности.Сам принцип формулируется так: никакими механическими опытами невозможно определить, движется ли система отсчёта равномерно и прямолинейно или покоится.
А вот СЛЕДСТВИЕМ такого принципа будет галилеевская формула сложения скоростей: скорость тела в некоторой системе отсчёта равна сумме его скорости в другой системе отсчёта и скорости второй системы отностиельно первой.