Работа силы на конечном перемещении

Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.

Работа силы на конечном перемещении М₁М₀ равняется интегралу вдоль этого перемещения от элементарной работы.

Работа силы на перемещении М₁М₂ изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М₁ и М₀.

Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).

Теоремы о работе силы

Теорема 1. Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Теорема 2. Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.

Работа и мощность при поступательном и вращательном движениях

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.

Элементарной работой силы называется величина, равная скалярному произведению силы на элеме

,

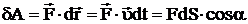где – элементарный путь точки приложения силы за время dt, a – угол между векторами и .

Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:

.

Если = const, то А= × .

При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:

,

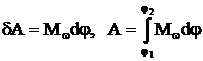если М_w = const, то А = М_w×j.

Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:

– средняя мощность; – мгновенная мощность.

При вращательном движении мощность определяется следующим образом:

.

Мощность равна:Р = А/t.

Пользуясь этой формулой, найдем мощность электрического тока. Так как работа тока определяется формулой А = IUt, то мощность электрического тока равна:Р = IU

За единицу мощности ватт (Вт) принята мощность тока силой 1 А на участке с напряжением 1 В. Следовательно, 1 Вт = 1 А·1 В.

14. Работа упругой и гравитационной сил. Консервативные силы.

Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.
На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой 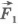(рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно . Вычислим работу силы упругости при перемещении шара из точки с координатой x1 в точку с координатой x2. Из рисунка 6.10, в видно, что модуль перемещения равен:

где - конечное удлинение пружины.

Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформациипружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком зависимости модуля силы упругости от координаты шара (рис.6.11).

В § 43 мы показали, что при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости Fx от x и что эта работа численно равна площади прямоугольника. При произвольной зависимости Fx отx, разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.
В нашем примере работа силы упругости на перемещении точки ее приложения численно равна площади трапеции ВCDM. Следовательно,

Согласно закону Гука и . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что , получим

Или окончательно

Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: . Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.
Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины 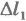и в начальном и конечном состояниях.
Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.