Неинерциальные системы отсчета. Сила инерции.

Неинерциальная система отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, покоится либо движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того, чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.

Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Классическая механика постулирует следующие два принципа: время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта; пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.

Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.

Уравнение движения материальной точки в неинерциальной системе отсчёта может быть представлено в виде:

или в развёрнутом виде:

где — масса тела, , — ускорение и скорость тела относительно неинерциальной системы отсчёта, — сумма всех внешних сил, действующих на тело, — переносное ускорение тела, — кориолисово ускорение тела, — угловая скорость вращательного движения неинерциальной системы отсчёта вокруг мгновенной оси, проходящей через начало координат, — скорость движения начала координат неинерциальной системы отсчёта относительно какой-либо инерциальной системы отсчёта.

Это уравнение может быть записано в привычной форме второго закона Ньютона, если ввести силы инерции:

— переносная сила инерции, 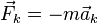— сила Кориолиса

В неинерциальных системах отсчета возникают силы инерции. Появление этих сил является признаком неинерциальности системы отсчета.

Сила инерции — фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем.
В математических вычислениях введения этой силы происходит путём преобразования уравнения F1+F2+…Fn = ma
к виду F1+F2+…Fn–ma = 0
Где Fn — реально действующая сила, а –ma — «сила инерции» .
Закон инерции про инерционные системы отсчёта гласит, что без влияния неуравновешенных сил тело будет сохранять свою скорость или неподвижность. В качестве примера силы инерции можно рассмотреть простую силу инерции, которую можно ввести в равноускоренной системе отсчёта:
Пусть у нас есть быстро останавливающийся автобус. Все тела в нём будут нарушать закон инерции — они будут иметь тенденцию продолжать движение, и пассажирам придётся крепко держаться за поручни, чтобы не упасть вперёд, и оставаться неподвижными на своих местах относительно автобуса. Но если предположить, что всем пассажирам приходится противодействовать некой силе, то можно будет объяснить эту тенденцию её действием. Такую силу и назвали силой инерции. С введением этой силы закон инерции в автобусе восстановится — тела можно счесть подвергающимися действию этой силы, и тогда они будут вести себя в полном соответствии со вторым законом Ньютона. Т. е. если пассажиры приложат к себе относительно поручней дополнительную мускульную силу, противоположную силе инерции, то останутся на своих местах.
Среди сил инерции выделяют следующие:
простую силу инерции, которую мы только что рассмотрели;
центробежную силу, объясняющую стремление тел улететь от оси во вращающихся системах отсчёта;
силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся