Классический метод расчёта переходных процессов

Классический метод расчёта основан на решении неоднородных дифференциальных уравнений, выражающих законы Кирхгофа для мгновенных значений токов и напряжений.

Например, переходной процесс в цепи, состоящей из последовательно соединённых R,L,С элементов при включении в неё источника ЭДС е(t) описывается уравнением:

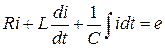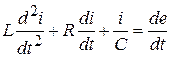или (6.3)

Решение уравнения (6.3) ищется в виде

,

где 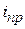- частное решение неоднородного уравнения

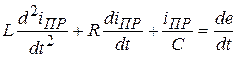, (6.4)

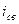- общее решение однородного дифференциального уравнения

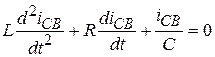. (6.5)

Функция 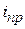зависит от вида воздействия и называется принужденнойсоставляющей реакции цепи. Она может быть найдена любым методом расчёта установившегося процесса.

(adsbygoogle = window.adsbygoogle || []).push({});

Функция 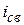не зависит от внешнего воздействия, определяется характером цепи, её начальными условиями и называется свободной составляющей реакции цепи (свободная составляющая тока).

В зависимости от параметров элементов цепи и соответственно вида корней характеристического уравнения, общее решение однородного дифференциального уравнения, приведенного в примере, ищется в виде:

1) корни характеристического уравнения действительные

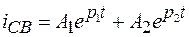, (6.6)

где А₁, А₂- постоянные интегрирования, определяемые из начальных условий; p₁, p₂ – корни характеристического уравнения.

В этом случае 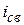изменяется по экспоненциальному закону (рис. 6.1а)

Рис. 6.1. Временная зависимость свободной составляющей тока в случае

а) действительных корней характеристического уравнения б) комплексно-сопряженных корней.

2) Корни характеристического уравнения комплексно-сопряженные p_1,2=d±jw

|-------------------------------------------------------------------------------------------------------------------------------|

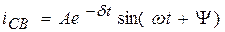
54) Переходные процессы в цепях переменного тока с индуктивностью и емкостью

|--------------------------------------------------------------------------------------------------------------------|

55) Разветвленная цепь переменного тока. Метод проводимостей

На практике часто используются разветвленные цепи, в которых необходимо рассчитать токи во всех ветвях и ток всей цепи, а также активную, реактивную и полную мощность цепи.

ЦЕПЬ ИЗ ДВУХ ПАРАЛЛЕЛЬНЫХ ВЕТВЕЙ.

Рассмотрим простейшую цепь переменного тока, состоящую из двух параллельных ветвей с последовательно включенными активными сопротивлениями и катушками индуктивности и подключенную к источнику синусоидального напряжения (рис.151). В соответствии с законом сохранения заряда сила мгновенного тока в неразветвленной части цепи будет равна сумме токов в параллельных ветвях .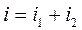

В каждой ветви ток будет отставать от напряжения на ветви (см. § 52), а напряжение на ветвях общее. Поэтому построим векторную диаграмму токов, считая, что мгновенные значения токов в первой и второй ветвях отстают от напряжения соответственно на 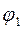и (рис.152).

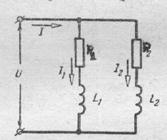
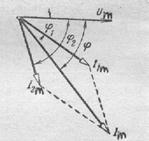
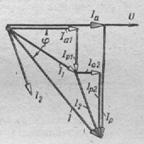
РИС.151 РИС.152 РИС.153 РИС.154

Амплитудные и действующие значения силы токов в ветвях можно найти, используя следующие соотношения:

, , , , .

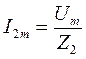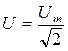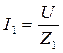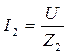Используя векторную диаграмму и эти соотношения, можно найти действующее значение силы тока и сдвиг фаз между током и напряжением:

,

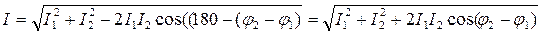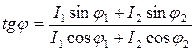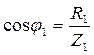, где и .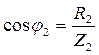

Соответственно можно рассчитать активные, реактивные и полные мощности ветвей: , , ,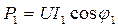

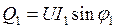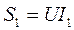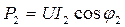, , , а также активную, реактивную и полную мощность всей цепи:

, , .

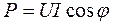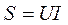Если в одной из ветвей будет включена емкостная нагрузка, то вектор силы тока в этой ветви будет опережать вектор напряжения на некоторый угол, а величина суммарного тока и сдвиг фаз будут определяться соотношением реактивных сопротивлений ветвей.

МЕТОД ПРОВОДИМОСТЕЙ.

Если в цепи больше двух параллельных ветвей, то для рационального расчета используется метод проводимостей, который основан на следующем.

1)Ток в каждой цепи является векторной суммой активной и реактивной составляющих (рис.153). Например, для рассмотренной выше цепи действующие значения токов в ветвях можно рассчитать по следующим формулам: ,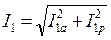

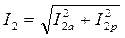
2)Активные составляющие совпадают по фазе с напряжением и равны: , ,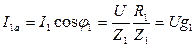

(adsbygoogle = window.adsbygoogle || []).push({});

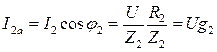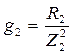, , где g₁ и g₂- активные проводимости первой и второй ветвей.

3) Реактивные составляющие токов отличаются по фазе от напряжения на 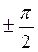и рассчитываются по формулам:

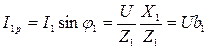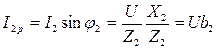, , , , где b₁ и b₂ – реактивные проводимости первой и второй ветвей.

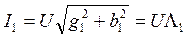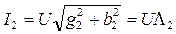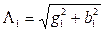Тогда: , , где и 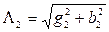- полные проводимости обоих ветвей.

Проводимость всей цепи может быть рассчитана по формуле :

, где g=g₁+g₂ и b=b₁+b₂ и представлена треугольником проводимостей (рис.154), который является следствием векторной диаграммы токов.

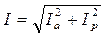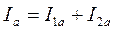4)Общая сила тока в цепи может быть рассчитана как модуль векторной суммы активной и реактивной составляющих , где и .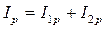

5)Сдвиг фаз между током и напряжением: 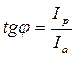или .

6)Активную, реактивную и полную мощность цепи можно рассчитать по формулам: , , ,

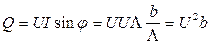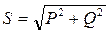
В общем случае разветвленной цепи применяют метод эквивалентных (равнозначных) схем, т.е. цепь последовательно упрощают, заменяя сопротивление разветвленных участков эквивалентными сопротивлениями. Для этого рассчитывают активные и реактивные проводимости параллельных ветвей, а затем полную проводимость и сопротивление разветвленного участка. В результате разветвленная цепь заменяется неразветвленной – эквивалентной. Затем рассчитывается ток, сдвиг фаз между током и напряжением, активная, реактивная и полная мощность цепи.

56) Активная, реактивная и полная мощности трехфазной цепи