Сложные суждения и их виды.

Сложные суждения образуются путём соединения между собой простых суждений при помощи логических союзов. Существует множество таких союзов, но главными из них в современной логике считаются следующие: конъюнкция, исключающая и не исключающая дизъюнкции, импликация и эквивалентность. В естественном языке они выражаются при помощи грамматических союзов «и», «либо…, либо», «или», «если…, то», «тогда, и только тогда».

1) соединительные;(конъюнктивные)-суждения объединенные связкойИ."Мой брат - студент юридического факультета, а сестра - студентка химического факультета. (союз а.)

2) разъединительные (дизъюнктивные); суждения объединённые разделительной связкой или, либо. -Например, «Клевета, соединенная с обвинением лица в совершении тяжкого или особо тяжкого преступления, наказывается ограничением свободы на срок до трех лет, либо арестом на срок от четырех до шести месяцев, либо лишением свободы на срок до трех лет».

3) условные (импликативные) - суждения образованы из двух простых суждений посредствам логического союза «если [...], то». Например, «Если по истечении срока временной работы с работником не был расторгнут договор, то он считается принятым на постоянную работу». Аргумент, начинающийся в таких суждениях словом «если», называется основанием, а со слова «то» - следствием. В таких суждениях отражаются причинно-следственные, пространственно-временные связи между предметами.

4) равнозначны или эквивалентные - выражаемой логической связкой «если и только если..., то...». Например: «Если и только если человек награжден орденами и медалями, то он имеет право на ношение соответствующих орденских планок». союзы: «лишь при условии что..., то...», «в том и только в том случае когда..., тогда...», «только тогда когда..., то...» и другие.

26 Таблицы истинности и их построение.

Таблица истинности – таблица, с помощью которой устанавливается значение истинности сложного суждения в зависимости от значения истинности простых суждений, входящих в его состав. Каждое из сложных суждений имеет свою таблицу истинности. В классической логике сводные данные для конъюнкции, дизъюнкции, импликации и эквиваленции имеют следующий вид. таблица значений истинности: буква «и» соответствует значению «истинно», буква «л» – значению «ложно». А и В

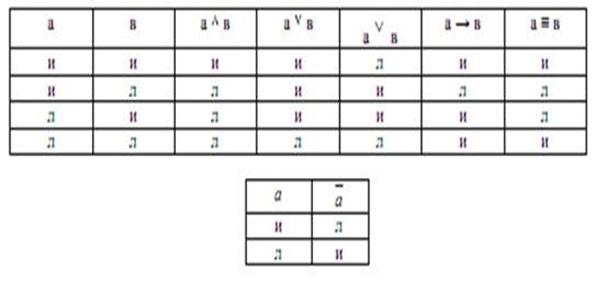
Выделяют следующие правила соотношения истинности и ложности суждений: 1. Из истинности общего, подчиняющего суждения следует истинность подчиненного частного суждения. 2. Из ложности общего суждения не вытекает ни истинность, ни ложность частного суждения, – оно остается неопределенным.

Алгоритм построения таблицы истинности: 1.Определить число переменных 2.Определить число строк в таблице истинности. 3.Записать все возможные значения переменных. 4.Определить количество логических операций и их порядок. 5.Записать логические операции в таблицу исинности и определить для каждой значения.