Примеры решения задач. 1. Движение тела массой 1кг задано уравнением: s = 6t3 + 3t + 2

1. Движение тела массой 1кг задано уравнением: s = 6t³ + 3t + 2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды движения.

Дано: m=1 кг; s = 6t³ + 3t + 2; t = 2 с.

Найти: F, v, а.

Решение. Мгновенную скорость находим как производную от пути по времени: ; v = 18t² + 3 Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени: а = 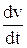= ; a = 36 t

Сила, действующая на тело, определяется по второму закону Ньютона: F = ma, где а, согласно условию задачи, есть ускорение в конце второй секунды. Тогда: F = m36t; F= 1∙ 36×2 = 72 кг∙м/с² =72 Н

Ответ: v = 18t² + 3; a = 36t; F = 72 H.

2. Стержень длиной 1 м движется мимо наблюдателя со скоростью

0,8 с. Какой покажется наблюдателю длина стержня?

Дано: l₀ = 1 м, v = 0,8 с.

Найти: l.

Решение. Зависимость длины тела от скорости в релятивистской механике выражается формулой: l = l₀ 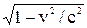, где l₀— длина покоящегося стержня; v — скорость его движения; с — скорость света в вакууме. Подставляя в формулу числовые значения, имеем: l =1∙ = 1∙ = 0,6 м.

Ответ: l = 0,6 м.

3. Две частицы движутся навстречу друг другу со скоростями:

1) v = 0,5 с и u = 0,75 с; 2) v = c и u = 0,75 с. Найти их относительные скорости в первом и во втором случаях.

Дано: 1) v = 0,5 с, u = 0,75 с; 2) v = c, и = 0,75 с. Найти: и^/_1, u^/₂.

Решение. Согласно теореме сложения скоростей в теории относительности:

;

где v, u — скорости соответственно первой и второй частиц; u' — их относительная скорость; с — скорость света в вакууме. Для первого и второго случаев находим: = 0,91 с; = с;

Это означает, во-первых, что ни в какой инерциальной системе отсчета скорость тела не может превзойти скорость света; во-вторых, скорость распространения света в вакууме одна и таже во всех инерциальных системах отсчёта.

Ответ: u¢₁ =0,91 с; u¢₂ = с.

4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол a = 60°, и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе.

Дано: m₁ = 0,5 кг, m₂ =1 кг, a=60°; l = 0,8 м. Найти: h, DE_д.

Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью v. Закон сохранения импульса при таком ударе имеет вид: m₁v₁ + m₂v₂ = (m₁ + m₂)v. (I)

1. Здесь v₁ и v₂ — скорости шаров до удара. Скорость большого шара до удара равна нулю (v₂ = 0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на yгол a ему сообщается потенциальная энергия, которая при отпускании шара переходит в кинетическую энергию: m₁gh₁= m₁v²₁/2. Из рисунка видно, что высота h₁ равна: h₁= l(1— cos a) = 2l sin² (α/2);

Отсюда: (2)

Из уравнений (1) и (2) находим скорость шаров после удара:

v = m₁v₁/(m₁ + m₂) = 2m₁ 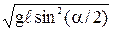(m₁ + m²) (3)

Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную при последующем подъеме обоих шаров на высоту h:

(m₁ + m₂)v²/2 = (m₁ + m₂)gh, (4)

Из формулы (4) находим: h = v²/2g, или с учетом (3):

h == 2m²₁lsin²(α/2)/(m₁ + m₂)² h = 2∙0,5²∙0,8∙0,25/(0,5 +1)² = 0,044 м.

При неупругом ударе часть энергии шаров расходуется на их деформацию. Энергия деформации определяется как разность кинетических энергий шаров до и после удара: ΔЕ_Д =( m₁v²₁/2) – (m₁ + m₂)v²/2.

Используя уравнения (2) и (3), получаем: ΔЕ_Д = 2glm₁ sin²(α/2);

ΔЕ_Д =2·9,81м/с²·0,8м·0,5кг(1-0,5кг/1,5кг)·0,25=1,3 Дж.

Ответ: h = 0,044 м, ΔЕ_Д = 1,3 Дж.

5. Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе c изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия. Систему молот—изделие—наковальня считать замкнутой.

Дано: m = 70 кг, m₂ = 1330 кг, h = 5 м.

Найти: Е_Д.

Решение. По условию задачи система молот—изделие—наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара.

Считаем, что во время удара изменяется только кинетическая энергия тел, т.е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем:

Е_Д = m₁v²/2 – (m₁ + m₂)v^{/ 2}/2, (1)

где v —скорость молота в конце падения с высоты h; v^/ —общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха по формуле

v = ; (2) Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения: = const. (3)

Для рассматриваемой системы закон сохранения количества движения имеет вид: m₁v = (m₁ + m₂)v^/, откуда: v^/ = m₁v/(m₁ + m₂) (4)

Подставив в формулу (1) выражения (2) и (4), получим:

Е_Д = m₁m₂gh/(m₁ + m₂); Е_Д = 70∙9,8∙5∙1330/(1330 + 70) = 325,85 Дж

Ответ: Е_Д = 325,85 Дж.

6. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением: s = 2t² + 4t + 1. Определить работу силы за 10 с, с начала ее действия и зависимость кинетической энергии от времени.

Дано: m = 1 кг, s = 2t² + 4t + 1.

Найти: A, T = f(t).

Решение. Работа, совершаемая переменной силой, выражается через интеграл (1). Сила, действующая на тело, по второму закону Ньютона равна: F = ma или F = m (2). Мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим находим:

v = = 4t + 4 (3); a = = 4 м/с². (4)

Тогда F = m = 4m (5). Из выражения (3) определим ds: ds = (4t+4)dt. (6). Подставив (5) и (6) в уравнение (1), получим: A = .

По этой формуле определим работу, совершаемую силой за время 10 с. с начала ее действия:

A = = m = 1(8∙100 + 16∙10) = 960 Дж.

Кинетическая энергия определяется по формуле: T = mv²/2; (7)

Подставляя (3) в (7), имеем:

T = m(4t + 4)²/2 = m(16t² + 32t + 16)/2 = m(8t² + 16t +8)

Ответ:A = 960 Дж, T = m(8t² + 16t +8).

7. Протон движется со скоростью 0,7 с (с - скорость света). Найти

импульс и кинетическую энергию протона.

Дано: v = 0,7 с; с = 3∙10 м/с, m = 1,67∙10^-27 кг. Найти: р, Т.

Решение. Количество движения или импульс протона определяется по формуле: p = m₀v/ 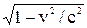= m₀v/ 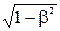; где m₀ —масса покоя протона; v — скорость движения протона; c — скорость света в вакууме; v/c = β — скорость протона, выраженная в долях скорости света.

p = 1,67∙10^-27∙3∙10⁸∙0,7/ = 4,91∙10^-19 кг·м/с.

В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Е и энергией покоя этой частицы:

Т = Е – Е₀, где Е = m₀c²/ 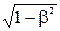; Е₀ = m₀c².

Подставив, имеем: Т = m₀c²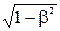(1/ - 1);

Вычисляем: T = 1,67∙10^-27∙(3∙10⁸)² (1/ - 1) = 0,6∙10^-10 Дж.

Ответ: р = 4,91∙10^-19 кг•м/с; Т = 0,6∙10^-10 Дж.

8. Какую наименьшую скорость нужно сообщить ракете, чтобы она, стартовав с Земли, не вернулась на Землю? Сопротивление атмосферы не учитывать.

Дано: R₃ = 6,37∙10⁶ м; g = 9,8 м/с²; R→∞.

Найти v .

Решение. С удалением ракеты от Земли будет увеличиваться ее потенциальная энергия и уменьшаться кинетическая. По закону сохранения энергии:

mv₀²/2 – mv²/2 = m(GM/R_З – GM/R), (1)

где m- масса ракеты; М-масса Земли; G - гравитационная постоянная; v₀ и v- скорость ракеты относительно Земли в начальный и рассматриваемый моменты; R₃ и R - расстояния от центра Земли до ракеты в начальный и рассматриваемый моменты; GM/R - потенциал гравитационного поля Земли на расстоянии R от ее центра. После преобразования уравнения (1) имеем:

v₀² - v² = 2GM(1/R_З - 1/R) ;

Ракета не вернется на Землю, если ее скорость v будет больше или равна нулю на бесконечно большом расстоянии от Земли: v = 0 при R → ∞. Отсюда:

v₀² = 2GM/R_З; (2) Из закона всемирного тяготения следует, что на поверхности Земли GmM/R_З² = mg, откуда GM = gR_З² (3), где g - ускорение свободного падения на поверхности Земли. Подставляя формулу (2) в (3), находим:

v₀ = . Считая, что ракета приобретает нужную скоростьv_o уже вблизи поверхности Земли, находим: v₀ = = 11,2 км/с.

Такая скорость необходима для преодоления гравитационного поля Земли. Она называется второй космической или параболической скоростью.

Ответ: v_о = 11,2 км/с.

9. Тело брошено вверх с высоты 12 м под углом 30° к горизонту с начальной скоростью 12 м/с. Определить продолжительность полета тела до точек А и В (cм. рисунок), максимальную высоту, на которую поднимается тело, и дальность полета тела. Сопротивление воздуха не учитывать.

Дано: H = 12 м, φ = 30°, v₀ = l2 м/с, g =9,8 м/с.

Найти: t_A, t_B, y_m, x_m.

Решение. В обозначенной на рис. системе координат проекции начальной скорости будут равны: v_ox = v₀cosφ (I), и v_0y = v₀sinφ (2).

y = H + v₀tsinφ – gt²/2 (3). x = v₀tcosφ (4).

Время подъема тела найдем из условия, что в наивысшей точке подъема скорость тела:

v_y = v₀sinφ – gt = 0 (2^/)

Тогда время подъема:

t_под = v₀sinφ/g (5).

Время спуска тела от точки С до точки А равно времени подъема, поэтому продолжительность полета тела от точки О , до точки А равна:

t_A = 2t_под =2v₀sinφ/g. (6)

Максимальную высоту подъема найдем из уравнения (3), подставив в него время подъема из уравнения (5):

y_m = H + v₀²sinφ²/2g (7)

Время полета тела до точки В найдем из уравнения (3), приравняв координату Y нулю (у = 0): t_B = v₀sinφ/g + (8)

Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (8): x_m = v₀t_Bcosφ (9) Тогда, решая совместно (6)-(9), получим:

t_A = 2∙12∙0,5/9,8 = 1,22 c. t_B = + = 2,29 c.

у_m = 12 + = 13,8 м. x_m = 12∙2,29∙0,867 = 23,8 м.∙

Ответ: t_A = 1,22 c, t_B = 2,29 c, у_m= 13,8 м, x_m = 23,8 м.∙

10. По условию задачи 9 найти в момент приземления тела следующие величины: скорость и угол падения тела, тангенциальное и нормальное ускорения тела, радиус кривизны траектории в точке В.

Дано: H = 12 м, φ = 30°, v₀ = 12 м/с.

Найти: v_B, β, a_n, R.

Решение. Мгновенная, скорость в точке B (см. рис.):

v_B = Проекцию скорости v_у в точке Bнайдем из уравнения (2') задачи (9), подставив в него время

движения t_B. из (8):

v_y = v₀sinφ – gt_B = .

Результирующую скорость v в точке В найдем как:

v = =

= =

= ; v = = 19,5 м/с.

Из рис. определим угол β, образуемый вектором скорости v c осью Оx:

sinβ = v_y/v = / ;

sinβ = 0,85; β = arc sin 0,85 = 57₀40^/.

Построим в точке В «треугольник ускорений». Вектор тангенциального ускорения a_τ направлен вдоль вектора мгновенной скорости в данной точке, т. е. по касательной к траектории; вектор нормального ускорения а_n перпендикулярен вектору мгновенной скорости v. Из рис. видно, что

a_τ = g sinβ = gv_y/v; a_n = g cosβ = gv_x cosφ/ ;

a_τ = 9,8∙0,85 = 8,3 м/с². a_n = 9,8∙12∙0,867/ = 5,25 м/с².

Радиус кривизны траектории в точке приземления (расстояние R = ОВ на рис.) определяем из уравнения: a_n = v²/R.

Отсюда имеем: R = v²/a_n; R = 19,5²/5,25 = 72,5 м.

Ответ: v = 19,5 м/с, β = 57°40', а_τ = 8,3 м/с², a_n = 5,25 м/с², R = 72,5 м.

11.Тонкий стержень массой 300 г и длиной 50 см вращается с угловой скоростью 10 c в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найти его угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдет через конец стержня.

Дано: m = 300 г = 0,3 кг, l = 50 см = 0,5 м, ω₁ = 10 c .

Найти: ω .

Решение. Воспользуемся законом сохранения момента импульса:

= сonst, (1) где J - момент инерции стержня относительно оси вращения. Для изолированной системы тел векторная сумма момента импульсов остается постоянной. В данной задаче вследствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменится. В соответствии с (1) запишем:

J₁ω₁ = J₂ω₂ (2)

Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен:

J₁ = J₀ = ml²/12. (3)

По теореме Штейнера: J = J₀ + md², где J - момент инерции тела относительно произвольной оси вращения; J₀ - момент инерции стержня относительно оси вращения, проходящей через центр масс; d - расстояние от центра масс до выбранной оси вращения. Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярно стержню:

J₂ = J₁ + md²; J₂ = ml²/12 + m(l/2)² = ml²/3 (4)

Подставим формулы (3) и (4) в (2): ml²ω₁/12 = ml²ω₂/3,

откуда: ω₂ = ω₁/4; ω₂ = 10/4 = 2,5 c^-1.

Ответ:. ω₂ = 2,5 c^-1

12.Маховик массой 4 кг свободно вращается с частотой 720 мин^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу с радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Дано: ω_t = 0, m = 4 кг, ν = 720 мин^{- 1}= 12с^-1; Δt = 30 с, R = 0,4 м.

Найти: М, N.

Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения: JΔω = МΔt, (I), где J - момент инерции маховика относительно оси, проходящей через центр масс; Δω— изменение угловой скорости за промежуток времени Δt.

По условию задачи, Δω=-ω₀, где ω₀ — начальная угловая скорость, так как конечная угловая скорость ω_t = 0. Выразим начальную угловую скорость через частоту вращения маховика, тогда ω₀ = 2πν и Δω = - 2πν. Момент инерции маховика J =mR², где m - масса маховика; R - его радиус. Тогда формула (1) примет вид: mR²2πν = - МΔt, откуда: М = - 2πνmR²/Δt.

Знак «-» свидетельствует о том, что момент силы является тормозящим.

M = 2∙3,14∙12∙4∙0,4²/30 = 1,61 Н∙м

Угол поворота, т. е. угловой путь φ, за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения:

φ = ω₀t – εΔt²/2, (2) где ε - угловое ускорeние. По условию задачи: ω = ω₀ – εΔt; ω_t = 0; εΔ t= ω₀. Тогда выражение (2) может быть записано в виде:

φ = ω₀Δ t- ω₀Δt/2 = ω₀Δt/2. Так как φ = 2πN; а ω₀ = 2πν, то число полных оборотов: N = νΔt/2; N = 12с^-1·30с/2 = 180.

Ответ: М = 1.61 Нм, N = 180 оборотов.

13. Определить, сколько киломолей и молекул водорода содержится в объеме 50 м³ под давлением 767 мм рт.ст. при температуре 18 ⁰С. Какова плотность и удельный объем газа?

Дано: V = 50 м³; р = 767 мм рт.ст.≈ 767·133 Па; Т = 18 + 273 = 291 К;

μ = 2·10^-3 кг/моль, R = 8,31 Дж/моль∙К, N_A = 6,025∙10²³ моль^-1.

Найти: ν, N, ρ, d.

Решение. На основании уравнения Менделеева – Клапейрона:

устанавливаем число молей ν, содержащихся в заданном объеме V. Зная р – давление, V – объем, Т – температуру газа, R –универсальную газовую постоянную определим ν: ν = ; ν = (кмоль).

Число молекул N, содержащееся в данном объеме газа, найдем, используя число Авогадро (которое определяет количество молекул содержащееся в одном киломоле вещества). Общее количество молекул, находящихся в массе m данного газа, может быть установлено по известному числу киломолей ν:

.

Подставив формулу числа киломолей, определяем число молекул, содержащихся в объеме V: N = 2,11·6,02·10²⁶ = 12,7·10²⁶.

Плотность газа ρ = m/V определяем из уравнения Менделеева – Клапейрона: pV = ; откуда находим: ρ = = .

Подставляя числовые значения в формулу, определим плотность газа:

ρ = (кг/м³).

Удельный объем газа d определяем из уравнения Менделеева – Клапейрона:

d = ; d = ≈ 11,9 (м³/кг).

Ответ: ν = 2,11 кмоль, N = 12,7·10²⁶, ρ = 8,44∙10^-2 кг/м³, d = 11,9 м³/кг.

14. В баллоне объемом 10 л находится гелий под давлением 1 МПа при температуре 300 К. После того как из баллона было выпущено 10 г гелия, температура в баллоне понизилась до 290 К. Определить давление гелия, оставшегося в баллоне.

Дано: V = 10^-2 м³; μ = 4·10^-3 кг/моль; р₁ = 10⁶ Па; ∆m = 10^-2 кг; Т₁ = 300 К;

Т₂ = 290 К; R = 8,31 Дж/моль∙К; N_A = 6,025∙10²³ моль^-1.

Найти: р₂.

Решение. Для решения задачи воспользуемся уравнением Менделеева – Клапейрона, применив его к конечному состоянию газа, учитывая, что объем газа не меняется: р₂V = , (1) где m₂ – масса гелия в баллоне в конечном состоянии; μ– масса одного киломоля гелия; R –универсальная газовая постоянная. Из уравнения (1) выразим искомое давление р₂: р₂ = . (2)

Массу гелия m₂ выразим через массу m₁, соответствующую начальному состоянию, и массу ∆m гелия, взятого из баллона: m₂ = m₁ - ∆m . (3)

Массу гелия m₁ найдем также из уравнения Менделеева – Клапейрона, применив его к начальному состоянию: m₁ = (4)

Подставляя в выражение (3) массу m₁ по формуле (4), а полученное выражение m₂ в формулу (2), найдем: р₂ = , или после преобразования и сокращения: р₂ = . (5)

р₂ = ≈ 3,64·10⁵ (Па).

Ответ: р₂ = 3,64·10⁵ (Па).

15 В резервуаре объемом 1,2 м³ находится смесь 10 кг азота и 4 кг водорода при температуре 300 К. Определить давление и молярную массу смеси газов.

Дано: V = 1,2 м³; m₁= 10 кг; μ₁ = 28·10^-3 кг/моль; m₂=4 кг;

μ₂ = 2·10^-3 кг/моль; Т=300 К, R = 8,31 Дж/(моль·К).

Найти: р, μ.

Решение. Определим парциальные давления р₁азота и р₂ водорода, воспользовавшись уравнением Менделеева – Клапейрона:

; (1) , (2)

где m₁ – масса азота; μ₁ – молярная масса азота; V – объем резервуара;

Т – температура газа; m₂ – масса водорода; μ₂ – молярная масса водорода.

По закону Дальтона: р = р₁ + р₂. (3)

Из уравнений (1) и (2) выразим р₁ и р₂ и подставим в уравнение (3):

Р = . (4)

Найдем молярную массу смеси газов по формуле: μ = , (5)

где m₁ – масса азота; m₂ – масса водорода; ν₁ – количество молей азота; ν₂ – количество молей водорода.

Количество молей азота и водорода v₁ и v₂ найдем по формулам:

; (6) . (7) Подставляя формулы (6) и (7) в выражение (5), найдем: μ = . (8)

Вычислим: (Па);

μ = (кг/моль).

Ответ: р = 4,9∙10⁶ Па, μ = 6∙10^-3 кг/моль.

16. Сосуд емкостью 2 л содержит азот при температуре 27 ⁰С и давлении 0,5 атм. Найти число молекул в сосуде, число столкновений между всеми молекулами за 1 с, среднюю длину свободного пробега молекул.

Дано: V = 2 л = 2·10^-3 м³; Т = 27 ⁰С = 300 К; р = 0,5 атм = 5,065·10⁴ Па; d = 3,1·10^-10 м; μ = 28·10^-3 кг/моль, N_А = 6,02·10²³ моль^-1; k = 1,38∙10^-23 Дж/К.

Найти: N, z, < λ >.

Решение. Число молекул в сосуде найдем исходя из уравнения Менделеева – Клапейрона: . В газе массой m содержится N молекул газа, так что m = Nm₀, где m₀ – масса отдельной молекулы. B одном киломоле вещества содержится число молекул, равное числу Авогадро N_А. Поэтому μ = m₀N_А и, следовательно: ; . (1)

Среднее число столкновений каждой молекулы с остальными за 1 с:

< z > = , где < v >= - средняя арифметическая скорость молекул газа. Средняя длина свободного пробега молекул газа < λ > равна:

< λ > = , где d – эффективный диаметр молекулы, n – концентрация молекул. Исходя из уравнения (1), . (2)

Общее число столкновений за 1 с равно: n·<z>.

Согласно уравнениям (1) и (2) имеем: . (3)

Средняя длина свободного пробега молекул: < λ > = . (4)

Вычисляем, подставив численные значения величин в системе СИ: ; (с^-1);

<λ>= (м)

Ответ: n = 2,45∙10²³ молекул, z = 2,5∙10⁹ с^-1, <λ> = 1,92∙10^-7 м

17. Определить коэффициент внутреннего трения для водорода, имеющего температуру 27 ⁰С.

Дано: Т = 27⁰С = 300 К; d = 2,3·10^-10 м; N_А= 6,02·10²³ моль^-1;

μ = 2·10 ^-3 кг/моль; R = 8,31 Дж/(моль·К).

Найти: η.

Решение. Из молекулярно-кинетической теории газов коэффициент внутреннего трения равен: , (1) где ρ – плотность газа, <v> - среднеарифметическая скорость; < λ > - средняя длина свободного пробега молекул. Плотность газа найдем из уравнения Менделеева – Клапейрона:

, (2) где m, V, р и Т – масса, объем, давление и температура газа, μ – молярная масса водорода. Среднеарифметическая скорость молекул равна: ; (3)

Средняя длина свободного пробега молекул равна: , (4)

где d – эффективный диаметр, n – концентрация молекул водорода. Давление и температура газа связаны следующим соотношением: , (5)

откуда: , (6) Постоянная Больцмана k связана с числом Авогадро N_A соотношением: . (7) Подставляя (2), (3) и (7) в уравнение (1), получим: .

(кг/м·с).

Ответ: η = 8,4∙10^-6 кг/м∙с.

18. Вычислить коэффициент внутреннего трения и коэффициент диффузии кислорода, находящегося при давлении 0,2 МПа и температуре 280 К.

Дано: р = 2·10⁵ Па; d = 2,9·10^-10 м; μ = 32·10^-3 кг/моль; Т = 280 К;

N_А= 6,02·10²³ моль^-1; k = 1,38·10^-23 Дж/К; R = 8,31 Дж/моль·К.

Найти: η, D.

Решение. На основании представлений молекулярно-кинетической теории газов коэффициент внутреннего трения идеального газа (динамическая вязкость) и коэффициент диффузии определяются по формулам:

< λ > < v >, (1) D = < λ > < v >, (2)

где ρ – плотность газа; <λ> - средняя длина свободного пробега и < v >- среднeарифметическая скорость молекул. Из (1) и (2) следует:

η = ρD. (3)

Среднeарифметическую скорость и среднюю длину свободного пробега молекул находим по формулам:

, (4) , (5)

где R –универсальная газовая постоянная; Т – термодинамическая температура; d – эффективный диаметр молекулы кислорода; n – концентрация молекул. Из основного уравнения молекулярно-кинетической теории газов определяем n: , (6) , где р – давление; k – постоянная Больцмана. Из (6) и (5), получаем: . (7)

Окончательный вид расчетной формулы для коэффициента диффузии найдем, подставляя выражения (4) и (7) в (2):

. (8)

Плотность кислорода определяется по формуле . С учетом (6) имеем:

. (9)

Подставляя (9) и (8) в (3), получаем расчетную формулу для коэффициента внутреннего трения: .

Делаем вычисления:

(м²/с);

(кг/(м·с)).

Ответ: D = 7,4∙10^-6 м²/с, η = 2∙10^-5 кг/(м∙с).

19. Вычислить количество льда, которое образуется в течение часа в бассейне, площадь которого 10 м². Толщина льда 15 см, температура воздуха –10 ⁰С, коэффициент теплопроводности льда χ = 2,1 Вт/(м·К).

Дано: S = 10 м²; Δх = 15 см = 0,15 м; t₁=-10 ⁰С; χ = 2,1 Вт/(м·К); t₂=0 ⁰С;

τ =1 ч = 3600 с; r= 3,35·10⁵ Дж/кг.

Найти: m.

Решение. Считаем процесс установившимся, температуру нижней поверхности льда равной 0 ⁰С, а верхней – температуре воздуха. Через слой льда от воды отводится тепло. Количество тепла Q, передаваемое через лед толщиной Δх, пропорционально градиенту температуры , площади передающей поверхности S и времени τ и определяется уравнением теплопроводности Фурье: .

Массу m образующегося льда определяем из уравнения для теплоты плавления Q льда, численно равной теплоте, отводимой от воды в процессе замораживания: Q = mr, где r – удельная теплота плавления льда.

Тогда: . (кг).

Ответ: m = 15 кг.