Примеры решения задач

1.Два шарика одинакового объема, обладающие массой 0,6·10^-3 г каждый, подвешены на шёлковых нитях длиной 0,4 м так, что их поверхности соприкасаются. Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60⁰. Найти величину зарядов и силу электрического отталкивания.

Дано: m = 0,6·10^-3 г = 0,6·10^-7 кг; l = 0,4 м; α= 60⁰; q₁ = q₂ =q.

Найти: q, F

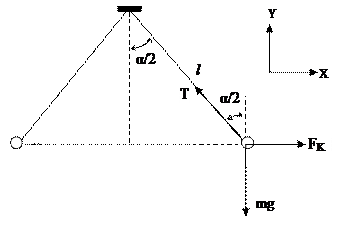Решение: В результате электростатического отталкивания заряды разойдутся на расстояние равное 0,4 м. Исходя из условия равновесия, запишем: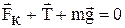

В проекциях на ось Х и ось Y получим:

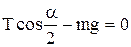(1) (2 )

Поделив первое уравнение на второе получим:

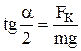, учитывая что 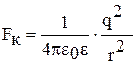или , где k₀ = ; получим: 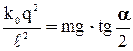, откуда .

Подставим данные: 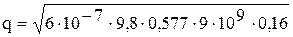= 7,8·10^-9 Кл.= 7,8 нКл

При этом сила отталкивания будет равна:

.

Ответ: F_к = 3,4·10^-6 Н., q=7,8 нКл

2. Вычислить ускорение, сообщаемое одним электроном другому, находящемуся в вакууме на расстоянии 1 мм от первого.

Дано: q = 1.6 · 10^-19 Кл; r = 1 мм = 10^-3 м.

Найти: а.

Решение. По закону Кулона электроны, находящиеся в вакууме на расстоянии r, взаимодействуют (отталкиваются) с силой ;

Под действием этой силы в соответствии со вторым законом Ньютона электрон приобретает ускорение: 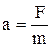, где m – масса электрона. Тогда ;

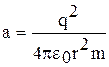≈ 2,5 10⁸ (м/с² ).

Ответ: а = 2,5∙10⁸ м/с² = 250 Мм/с².

3 .Заряды по 1 нКл помещены в вершинах равностороннего треугольника со стороной 0,2 м. Равнодействующая сил, действующих на четвертый заряд, помещенный на середине одной из сторон треугольника, равна 0,6 мкН. Определить этот заряд, напряженность и потенциал поля в точке его расположения.

Дано: q₁ = q₂ = q₃ = q = 1нКл = 10^-9 Кл; F = 0,6 мкН = 0,6∙10^-6 Н;

а = 0,2 м; ε₀ = 8,85∙10^-12 Ф/м.

Найти: q_Х, Е, φ.

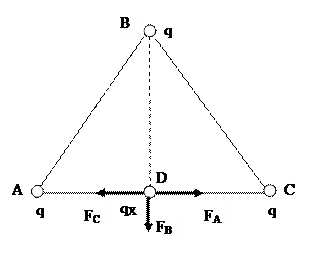Решение. Предположим, что в вершинах равностороннего со сторонами «а» треугольника АВС находятся одинаковые положительного знака заряды q, которые создают электрическое поле в точке D, расположенной на середине одной из сторон «а». Пусть в точке D находится положительного знака неизвестный заряд q_Х. Равнодействующая сил, действующих на заряд q_Х, равна векторной сумме кулоновских сил со стороны зарядов q, находящихся в точках А, В и С (см. рисунок): _А.+ _В + _С. Как следует из рисунка, кулоновские силы F_А и F_С одинаковые по величине (в силу равенства зарядов q и расстояний AD = АС = а/2), но противоположны по направлению, и их векторная сумма равна нулю. В результате равнодействующая сил от трех зарядов, будет равна кулоновской силе, действующей на заряд q_Х со стороны заряда q, находящегося в точке В: F = F_B.

Поскольку заряды q и q_Х являются точечными, то можно записать:

, (1) где r – расстояние между зарядами q и q_X. Как следует из рисунка: r = BD= (2) Подставив (1) в (2) имеем: q_X = . Вычисления дают:

q_X = = 2∙10^-9 Кл.

Напряженность является силовой характеристикой электрического поля и связана с кулоновской силой, действующей на заряд q_X, соотношением:

E = F/q_X. (3) Найдем значение поля Е в точке D: E = .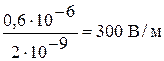

Потенциал является энергетической характеристикой электрического поля, поэтому потенциал поля в точке D будет равен алгебраической сумме потенциалов от зарядов q, находящихся в точках А, В и С:

φ = φ_А + φ_В + φ_С. (4)

Потенциал поля от точечного заряда равен: 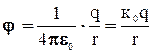, где r – расстояние от точки, в которой рассчитывается потенциал, до точечного заряда. Следовательно, потенциал поля в точке D в силу уравнения (4) будет равен:

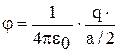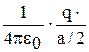+ + = . Отсюда:

φ = ; (5) Подставив численные значения физических величин в (5) имеем: φ = 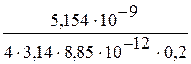= 231 В.

Ответ: q_X = 2∙10^-9 Кл, Е = 300 В/м, φ = 231 В.

4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии

а₁ = 0,5 см и а₂ = 2 см от поверхности цилиндра, в средней его части.

Дано: R = 1 см = 10^-2 м, τ = 20 нКл/м = 20∙10^-9 Кл/м, a₁ = 0,5 см, a₂ = 2 см.

Найти: φ₁- φ₂.

Решение. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала: .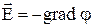

Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде: , или dφ =-Edr.

Интегрируя полученное выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r₁ и r₂ от оси цилиндра : φ₁ – φ₂ 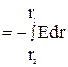(1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром: .

Подставив это выражение Е в (1), получим: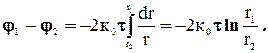

Или: 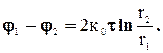(2)

Подставим числовые значения. Так как величины r₁ и r₂ входят в формулу (2) в виде отношения, то их можно выразить в любых, но одинаковых единицах: r₁ 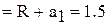см; r₂ 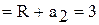см.

Следовательно: = 250 В.

Ответ: φ₁ – φ₂ = 250 В.

5. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью v₁ = 10⁶ м/с, чтобы скорость его возросла в 2 раза.

Дано: v₁ = 10⁶ м/с, n = 2, m = 9,1∙10^-31 кг, e = 1,6∙10^-19 Кл.

Найти: U.

Решение. Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля по переносу заряда (электрона). Эта работа определяется произведением заряда электрона e на разность потенциалов U:

А = eU. (1)

Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона: 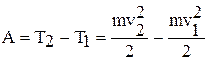, (2)

где T₁ и T₂- кинетические энергии электрона до и после ускорения в поле; m- масса, а v₁ и v₂ начальная и конечная скорости электрона.

Приравняв правые части равенств (1) и (2), получим: 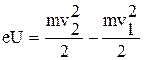, или:

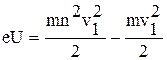, где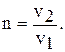

Отсюда искомая разность потенциалов: 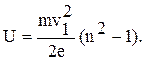(3)

Подставив числовые значения физических величин, имеем:

Ответ: U = 8,53 В.

6. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности потенциалов. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором, емкость которого С₂ = 5 мкФ. Какая энергия ∆W израсходуется на образование искры в момент присоединения второго конденсатора?

Дано: С₁ = 3 мкФ, С₂ = 5 мкФ, U₁= 40 В.

Найти: ∆W.

Решение. Энергия ∆W, израсходованная на образование искры: 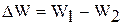(1), где W₁- энергия которой обладает первый конденсатор до присоединения к нему второго конденсатора; W₂- энергия, которую имеет батарея, составленная из первого и второго конденсаторов.

Энергия заряженного конденсатора определяется по формуле: 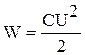, (2)

где С- емкость конденсатора или батареи конденсаторов; U- разность потенциалов на обкладках конденсаторов. Подставив в (1) энергии W₁ и W₂ из (2) и принимая во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим:

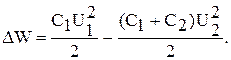(3), где С₁ и С₂- емкости первого и второго конденсаторов; U₁- разность потенциалов; до которой был заряжен первый конденсатор; U₂- разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежний, выразим разность потенциалов U₂ следующим образом: 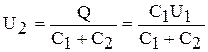. Подставив выражение U₂ в формулу (3), получим: После простых преобразований найдем:

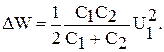
В полученное выражение подставим числовые значения и вычислим ∆W:

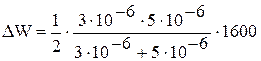= 1,5 мДж.

Ответ: ∆W = 1,5 мДж.

7. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с. по линейному закону от I₀ = 0 до I = 6 А . Определить теплоту Q₁, выделившуюся в этом проводнике за первую и Q₂-за вторую секунды, а также найти отношение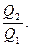

Дано: R = 20 Ом; Δt = 2 с; I₀ = 0; I = 6 A.

Найти: Q₁, Q₂,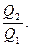

Решение. Запишем закон Джоуля-Ленца в виде: dQ = I²Rdt. (1)

Здесь сила тока I может являться некоторой функцией времени. В нашем случае ток линейно зависит от времени: I = kt (2)

где k – коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т.е. 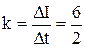= 3 А/с.

С учетом (2) формула (1) примет вид: (3)

Для определения теплоты, выделившейся за промежуток времени 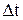, выражение (3) необходимо проинтегрировать в пределах от t₁ до t₂:

При определении теплоты, выделившейся за первую секунду, необходимо взять пределы интегрирования t₁ = 0, t₂ = 2 c. Следовательно:

Q₁ = 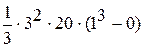= 60 Дж.

При определении теплоты, выделившейся за вторую секунду, необходимо взять пределы интегрирования t₁ = 1, t₂ = 1 c. Следовательно:

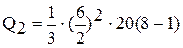= 420 Дж.

Таким образом, за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду. Следовательно: .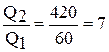

Ответ: Q₁ = 60 Дж, = 420 Дж, .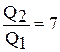

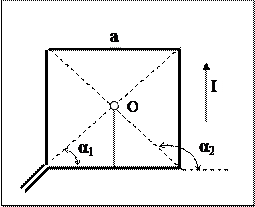
8. По проводу, согнутому в вид квадрата со стороной, а = 10см, течет ток силой I = 100A. Найти индукцию В магнитного поля в точке пересечения диагоналей квадрата.

Дано: I = 100 А; а = 10 см = 0,1 м; μ₀ = 4π∙10^-7 Гн/м.

Найти: В.

Решение: Расположим квадратный контур в плоскости чертежа (см. рисунок). Согласно принципу суперпозиции индукция В магнитного поля от квадратного витка будет равна векторной сумме индукций магнитных полей, создаваемых каждой стороной квадрата в отдельности:

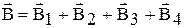(1)

В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости контура ‹‹к нам››. Кроме того, из соображений cимметрии следует, что абсолютные значения этих векторов одинаковы:

В₁ = В₂ = В₃ = В₄. Это позволяет векторное равенство (1) заменить скалярным равенством: В = 4В₁. (2)

Магнитная индукция В₁ поля, создаваемого отрезком прямолинейного провода с током, выражается формулой: (3)

Учитывая, что и 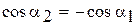(смотри рисунок), формулу (3) можно переписать в виде: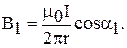

Подставив это выражение для В₁ в формулу (2), найдем:

Заметив, что 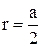и 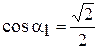(так как ), получим: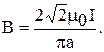

Подставим в полученную формулу числовые значения физических величин:

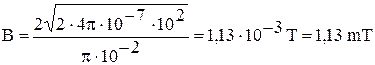л

Ответ: В = 1,13∙10^-3 Tл.

8. Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100 A, свободно установился в однородном магнитном поле индукцией В = 1 Т. Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) φ₁ = 90⁰; 2) φ₂ = 3⁰. При повороте контура сила тока в нем поддерживается неизменной.

Дано: I = 100 А, В = 1 Т, а = 10 см = 0,1 м, φ₁ = 90⁰, φ₂ = 3⁰.

Найти: А₁, А₂.

Решение. Как известно, на контур с током в магнитном поле действует момент сил: 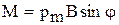(1), где - магнитный момент контура; В- магнитная индукция; φ - угол между вектором , направленным по нормали к контуру, и вектором .

По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (М = 0), а значит, φ = 0, т.е. вектора 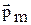и 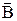совпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешних сил. Так как момент сил зависит от угла поворота φ, то для подсчета работы применим формулу работы в дифференциальной форме: 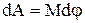. Подставив в это выражение М по формуле (1) и учитывая, что p_m = IS = Ia², где I – сила тока в контуре; S = a² – площадь контура, получим 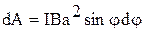. Взяв интеграл от этого выражения, найдем работу при повороте рамки с током на конечный угол φ: 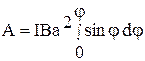(2)

Вычислим работу при повороте рамки на угол φ ₁= 90⁰:

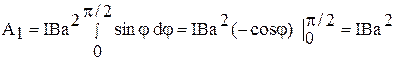. (3)

Подставим в (3) числовые значения величин: 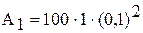= 1 Дж.

Вычислим работу при повороте рамки на угол φ₂ = 3⁰. Поскольку угол φ₂ мал, воспользуемся соотношением: sin φ ≈ φ и подставим его в выражение (2):

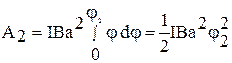. (4)

Подставим числовые значения величин в (4), предварительно выразив угол φ₂ в радианах:

= 1,37·10^-3Дж = 1,37 мДж.

Отметим, что задача могла быть решена и другим способом. Известно, что работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур: 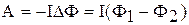, где Ф₁ – магнитный поток, пронизывающий контур до перемещения а Ф₂–после перемещения. В случае φ₁ = 90⁰ Ф₁ = BS, Ф₂ = 0: , что совпадает с полученным выше результатом (смотри формулу (3)).

Ответ: А₁ = 1 Дж, А₂ = 1,37∙10^-3 Дж.

10. Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле напряженностью H=10³ А/м. Определить радиус R кривизны траектории и частоту ν обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Дано: U = 400 В; Н = 10³ А/м; α = 90⁰; m = 9.11∙10^-31 кг; е = 1,60∙10^-19 Кл; Гн/м.

Найти: R, ν.

Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца 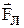(действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное (центростремительное) ускорение: :

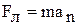(1), где е- заряд, v- скорость, m- масса электрона; В- индукция магнитного поля; R- радиус кривизны траектории; - угол между направлением вектора скорости и вектором . Из формулы (1) найдем: 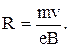(2)

Входящий в равенство (2) импульс mv может быть выражен через кинетическую энергию электрона: 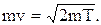(3)

Но кинетическая энергия электрона, проходящего ускоряющую разность потенциалов U, определяется равенством:

Подставив это выражение в формулу (3), получим:

Индукция В может быть выражена через напряженность H магнитного поля в вакууме соотношением: 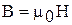, где - магнитная постоянная.

Подставив найденные выражения В и mv в формулу (2),найдем 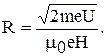(4)

Подставим числовые значения в формулу (4) и произведем вычисления:

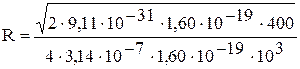= 5,37∙10^-2 м = 5,37 см.

Для определения частоты обращения ν воспользуемся формулой, связывающей частоту со скоростью движения электрона и радиусом траектории: 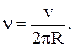(5)

Подставив в формулу (5) выражение (2) для радиуса кривизны, получим:

, или .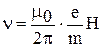

Подставим все величины, в системе СИ и произведем вычисления:

Ответ: ν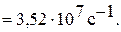

11. Резонанс в колебательном контуре, содержащем конденсатор емкостью С₁ = 1 мкФ, наступает при частоте ν₁ = 400 Гц. Когда же параллельно конденсатору С₁ подключили еще один емкостью С₂, резонансная частота становится равной ν₂ = 100 Гц. Найти емкость конденсатора С₂.

Дано: С₁ = 1 мкФ = 10^-6 Ф; ν₁ = 400 Гц; ν₂ = 100 Гц.

Найти: С₂.

Решение: Резонанс в колебательном контуре наступает, когда собственная частота колебаний становится равной частоте вынужденных колебаний, возбуждаемых внешним передатчиком. При этом амплитуда электромагнитных колебаний в контуре становится максимальной. Частота вынужденных колебаний, равная собственной частоте колебательного контура, называется резонансной частотой. Резонансная частота ν₁ в колебательном контуре, содержащем только один конденсатор С₁, определяется формулой Томсона: (1), где L – индуктивность катушки колебательного контура. Когда к конденсатору С₁ подключили параллельно конденсатор С₂, емкость батареи конденсаторов стала равна С₁+С₂. Резонансная частота ν₂ при этом равна: (2)

Обе частоты ν₁ и ν₂, а также емкость С₂ известны. Неизвестна индуктивность катушки L и искомая емкость С₂. Следовательно, необходимо исключить из уравнений (1) и (2) индуктивность L, например, поделив левые и правые части этих уравнений соответственно друг на друга. После деления, сокращения и упрощения получаем: ,

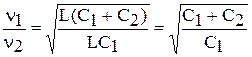
Отсюда ; .

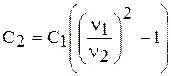Задача в общем, виде решена. Проведем вычисления:

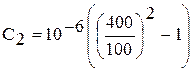= 1,5·10^-5 Ф.

Ответ: С₂=1,5·10^-5 Ф.

12. Максимум энергии излучения абсолютно черного тела приходится на длину волны 450 нм. Определить температуру и энергетическую светимость тела.

Дано: λ_maх = 450 нм = 4,5·10^-7 м; b = 2,89·10^-3 м·К; σ = 5,67·10^-8 Вт/(м²·К⁴).

Найти: Т, R.

Решение. Длина волны λ_max, на которую приходится максимум энергии излучения черного тела, по закону Вина равна: λ_max = .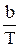

Отсюда: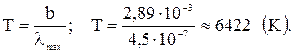

В соответствии с законом Стефана – Больцмана энергетическая светимость R абсолютно черного тела равна: R = σT⁴. В результате вычислений имеем:

Ответ: Т = 6422 К, R = 9,6∙10⁷ Вт/м².

13. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.

Дано: λ_к=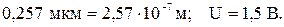

Найти: λ.

Решение. Согласно уравнению Эйнштейна для внешнего фотоэффекта:

Е_кmax. (1)

Красная граница фотоэффекта определяется из условия равенства энергии фотона работе выхода электронов А_В, т. е. 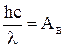. (2)

Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов U_з: Е_кmax= eU₃, (3)

где е – заряд электрона.

Подставляя выражения (2) и (3) в (1), получим: 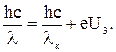(4)

Из уравнения (4) найдем длину волны света:

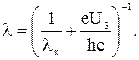(5)

Подставляя в (5) числовые значения, получим:

Ответ: λ = 0,196 мкм.

14. Определить максимальную скорость электрона, вырванного с поверхности металла γ – квантом с энергией 1,53 МэВ.

Дано: Е = 1,53 МэВ; Е₀ = 0,511 МэВ.

Найти: v_max,

Решение: По формуле Эйнштейна для фотоэффекта: Е = А_вых+Е_к.max.. Энергия кванта излучения расходуется на работу вырывания электрона А_вых и сообщение ему кинетической энергии Е_к.max.. Так как А_вых<< Е, то электрон будет релятивистским и Е 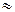Е_к, а кинетическая энергия будет выражаться формулой:

где Е₀ – энергия покоя электрона.

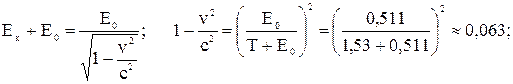
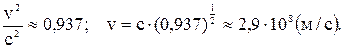
Ответ: v = 2,9∙10⁸ м/с.

15. Вычислить дефект массы, энергию связи и удельную энергию связи ядра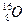

Дано: m = 1.00783 а.е.м.; m_n = 1,00867 а.е.м.; m = 15,99492 а.е.м.;

Z = 8; А = 16.

Найти: Δm, Е_св, ε_св.

Решение. Дефект массы Δm ядра определяется по формуле:

Δm = Zm_p + (A-Z)m_n - m_я. (1)

В таблицах чаще всего приводят массу атомов (изотопов), т.е. суммарную массу ядра вместе с электронами, то формулу (1) можно записать также в виде:

Δm = Zm + (А-Z)m_n - m_a, (2)

где m_a-масса изотопа, дефект массы ядра которого необходимо определить.

Подставляя в (2) числовые данные, получим: Δm = 0,13708 а.е.м.

Энергия связи ядра Е_св определяется по формуле:

Е_св = с²Δm. (3)

Если дефект массы Δm выражать в а.е.м., а энергию связи Е_св в МэВ, то формула (3) примет вид:

Е_св = 931 Δm (МэВ) (4)

Подставляя в (4) числовые значения, получим: Е_св = 931·0,13708 ≈ 128 (МэВ).

Удельная энергия связи ε_св вычисляется по формуле:

ε_св= . (5)

Проведя вычисления, получим: ε_св = 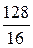= 8 (МэВ).

Ответ: Δm = 0,13708 а.е.м., Е_св = 128 МэВ, ε_св =8 МэВ.

16. Вычислить энергию ядерной реакции: 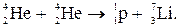Выделяется или поглощается энергия при этой реакции?

Решение. Энергия ядерной реакции определяется по формуле:

Q = c²(m₁ + m₂ - ∑m_i), (1)

где m₁ и m₂ - массы ядер и частиц, вступающих в ядерную реакцию, ∑m_i-сумма масс ядер и частиц, образовавшихся в результате реакции. Если массу частиц выражать в а.е.м., а энергию реакции в МэВ, то формула (1) примет вид:

Q = 931(m₁ + m₂ - ∑m_i). (2)

При вычислении энергии ядерной реакции можно использовать массы атомов вместо масс их ядер. Из справочных данных находим:

а.е.м., а.е.м., а.е.м.

Дефект массы реакции равен: Dm = (2 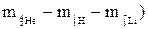= - 0,01864 а.е.м.

Подставляя значение дефекта массы реакции в (2), получим:

Q = 931(-0,01864) ≈ -17,4 (МэВ).

Поскольку Q < 0, то для осуществления такой реакции необходима энергия.

Ответ: Q = -17,4 МэВ.