Добротность, логарифмический декремент затухания

Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания:

Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (3.28) β через λ, и T, можно закон убывания амплитуды со временем записать в виде

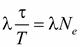За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить N_e = τ/T колебаний. Из условия получается, что . Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в e раз.

Для характеристики колебательной системы часто употребляется также величина называемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебаний N_e, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в e раз.

Чем больше добротность, тем медленнее затухают колебания осциллятора.