Теоретическое введение

Жидкость – это состояние вещества, промежуточное между газом и твердым телом. В газах все межмолекулярные связи разорваны, отдельные молекулы разлетаются и движутся независимо одна от другой. Поэтому газы могут занимать любой объем, а их плотность мала.

В твердых телах между молекулами (атомами) действуют силы притяжения, вы­страивающие их в упорядоченную струк­туру. Такие связи, обозначены на рис. 1 штриховыми линиями, а вызвавшие их силы притяжения имеют электростатическую или квантовую природу.

В жидкости большое число связей ра­зорвано (рис. 2). Но оставшиеся связи, по-прежнему, удерживают отдельные молекулы вместе, не позволяя им разлететься как в га­зах. Отдельные молекулы связаны в макромолекулы или молекулярные слои, и объем и плотность жидкости не слишком не слишком отличаются от объема и плотности твердого тела.

Тем не менее, разорванных связей много, и отдельные моле­кулы могут легко оторваться от одной макромолекулы и присоеди­ниться к другой в месте пустой ра­зорванной связи (вакансии). Это приводит к тому, что молекулы жидкой среды могут легко сме­щаться, а жидкость деформиро­ваться, т.е. менять форму при не­изменном объеме, течь.

Заметим, что межмолекулярные силы , действующие на молекулу А в глубине жидкости в целом уравновешивают друг друга, а силы, действующие на молекулу Б на поверхности жидкости, стремятся втянуть ее вглубь (рис. 2). Это приводит к появлению поверхностного слоя вблизи границы жидкости. Физиче­ские свойства поверхностного слоя отличаются от свойств остального объема жидкости. Толщина поверхностного слоя не превышает размера макромолекул ~ 0,1 ÷ 1,0 мкм. Межмолекулярные силы стремятся уменьшить площадь поверх­ностного слоя, втянуть все молекулы из этого слоя в объем жидкости. Такое явление называется поверхностным натяжением, а результирующие всех межмолекулярных сил, т.е. силы, действующие на поверхностный слой жидкости, называются силами поверхностного натяжения.

Свободная поверхность жидкости – это та поверхность, которая может дефор­мироваться, т.е. изменять свою форму и размер. Она существует, например, на гра­нице жидкость – воздух. Силы поверхно­стного натяжения всегда направлены по касательной к свободной поверхности (поверхностному слою) жидкости и стремятся сократить ее площадь.

Так как каждый кусочек свободной поверхности жидкости, заштрихованной на рис. 3, уравновешен, то результирующие силы поверхностного натяжения прило­жены к контуру, ограничивающему свободную поверхность и направлены перпендикулярно к этому контуру.

Величину этих сил можно определить с помощью коэффициента поверхно­стного натяжения , который численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего свободную поверхность (рис. 3):

. (1)

Увеличим площадь поверхностного слоя, оттянув участок его границы длины на расстояние dx (рис. 4). Для этого надо со­вершить работу против сил поверхностного натяжения:

, (2)

где – изменение площади поверхно­сти. Заметим, что если таким образом растя­гивать тонкую пленку на рамке, то величина работы (3) удваивается, т.к. у пленки по­верхность существует с двух сторон.

Все фазовые переходы, включая рост одной фазы и уменьшение другой, в том числе образование и рост поверхности раздела фаз или поверхностного слоя происходят при неизменной температуре Т, т.е. изотермически.Поэтому приходим к другому определению коэффициента поверхностного натяжения – это работа, которую надо совершить при неизменной температуре для увеличения площади поверхности на единицу:

. (3)

Эта работа идет на изменение потенциальной энергии. Действительно, из рис. 2 видно, что при растягивании поверхностного слоя надо добавить в него молекулы А из глубины жидкости, совершая работу против межмолекулярных сил . Молекулы в поверхностном слое обладают большей энергией, чем молекулы в объеме жидкости.

Сила поверхностного натяжения

. (4)

т.е. коэффициент поверхностного натяжения равен свободной энергии единицы площади поверхностного слоя жидкости.

Заметим, что способная превращаться в механическую работу свободная энергия будет потенциальной энергией поверхностного слоя. Связанная энергия поверхности является скрытой теплотой образования поверхности. При увеличении или уменьшении площади поверхности энергия выделяется или поглощается в виде теплоты.

Свободный поверхностный слой возникает на границе раздела любых фаз: жидкость-газ, жидкость-жидкость, жидкость–твердое тело и т.п. Его форма определяется условием равновесия всех сил, включая силы поверхностного натяжения. Так на краю трубки или капилляра, наполненного жидкостью с плотностью 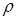, появляется капля с поверхностью довольно сложной формы (рис.5). Пусть радиус трубки равен r, а высота жидкости в ней равна h.

Свободная поверхность капли ограничена контуром длины – это окружность, про­ходящая по линии раздела трех сред: жидкость–воздух–твердое тело (стенки трубки). Силы по­верхностного натяжения направлены перпенди­кулярно к этой окружности, по касательной к по­верхности капли и стремятся уменьшить ее пло­щадь, т.е. направлены вверх (рис. 5). В общем случае угол между поверхностью капли и стенками трубки не равен нулю. Этот угол назы­вается краевым.

Выделим верхнюю поверхность капли с объемом V и массой (заштрихованное на рис. 5 сечение площадью ).

Капля медленно растет. Её центр масс С смещается вниз, и потенциальная энергия жидкости уменьшается. Но одновременно увеличивается площадь поверхности капли и её свободная энер­гия (8). Суммарная потенциальная энергия остается минимальной:

. (5)

Именно это условие определяет рост и форму капли.

В момент её отрыва, который про­исходит в шейке капли (рис. 6), сила поверхностного натяжения, приложенная к контуру, охватывающему шейку, урав­новешена силой тяжести:

или ,

где R – радиус шейки, V – объём капли, находящейся ниже шейки. Отсюда нахо­дим:

. (6)

При малейшем увеличении объема V капли шейка рвется, капля летит вниз, а на краю трубки начинает образовываться новая капля.

Измерить радиус R шейки капли очень сложно (например, фотографируя каплю в момент отрыва). Поэтому в данной работе применяется сравнительный способ использования формулы (6).

При одинаковом радиусе r трубки геометрические размеры главных радиусов кривизны R и 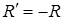на рис. 6 будут одинаковы для капель любой жидкости. Т.е. можно считать радиус шейки R капли в момент отрыва практически одинаковым для любых капель жидкости. Тогда, используя эталонную жидкость (например, дистиллированную воду) с известным коэффициентом поверхностного натяжения 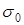и плотностью , можно записать

. (7)

Если из трубки вытекают в виде капель одинаковые объемы эталонной и исследуемой жидкости, то

, (8)

где, соответственно, 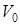и V – объемы капель, и N – подсчитываемое число капель этих жидкостей. Взяв отношение формул (6) и (7) и используя связь (8), получим:

, откуда . (9)

Заметим, что поверхностное натяжение жидкостей сильно уменьшается с ростом температуры Т. Поэтому сравнивать истечение жидкостей и измерять величину надо при постоянной (комнатной) температуре.

Кроме того, на вытекание капель может повлиять вязкость жидкостей. Поэтому используемый метод можно применять только при сравнении жидкостей с приблизительно одинаковой и малойвязкостью.

Лабораторная установка представляет собой укрепленную на вертикальном штативе капельницу. Капельница – это стеклянная трубка с узким нижним концом. Перед узкой частью трубки имеется кран, которым регулируется истечение жидкости из капельницы. На трубке нанесены деления, позволяющие определять объем протекающей жидкости.