Теоретическое введение. Многие процессы в организме являются периодическими

Многие процессы в организме являются периодическими. Некоторые из них можно рассмотреть как колебательные. Колебательным называется движение, повторяющееся через определенные промежутки времени. Промежуток времени Т, в конце которого система оказывается в том же положении и движется с той же скоростью, как и в его начале, называется периодом колебаний. Величина, обратная периоду, называется частотой колебаний ; частота определяет, сколько раз в секунду повторяются колебания. Среди разнообразных колебаний, встречающихся в природе и организме человека, существенную роль играют гармонические колебания. Гармонические колебания представляют собой периодический процесс, в котором изменение величины происходит по закону косинуса (или синуса):

,

где – амплитуда, т.е. максимальное отклонение изменяющейся по гармоническому закону величины от среднего значения; – фаза колебания; – начальная фаза; – циклическая (круговая) частота (число колебаний за секунд). Пусть гармонические колебания вдоль оси Х совершает материальная точка массой m. Найдем силу, которая при этих условиях будет на нее действовать.

Найдем проекцию скорости точки на ось Х

.

Тогда проекция ускорения на ось Х будет

.

По второму закону Ньютона или (1)

где k – постоянный коэффициент. Обозначим

, (2)

где – собственная частота колебаний. Таким образом, чтобы материальная точка совершала гармонические колебания, действующая на неё сила должна быть пропорциональна х и направлена в сторону, противоположную смещению х. Такая сила называется квазиупругой.

Математическим маятником называется материальная точка на длинной нерастяжимой невесомой нити, совершающая под действием силы тяжести колебания относительно оси Z. Отклоним маятник от положения равновесия на небольшой угол и отпустим. Возникает вращающий момент , проекция которого на ось Z равна , где 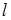– длина нити маятника. При малых углах можно принять . Тогда уравнение вращательного движения для маятника запишется в виде

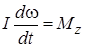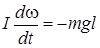или (3)

Сравнивая (1) и (3) видим, что аналогией квазиупругой силы является момент силы, роль коэффициента k играет величина mgl , а роль массы момент инерции I. Таким образом, по аналогии можно записать выражение для собственной частоты математического маятника . Тогда период колебаний для математического маятника (формула Гюйгенса)

. (4)

Период колебаний математического маятника не зависит от его массы, а зависит от его длины и ускорения свободного падения. Таким образом, измеряя период колебания математического маятника, можно найти ускорение свободного падения в данной точке земного шара:

l. (5)

Поскольку Земля имеет форму несколько сплюснутого шара и ее полюса расположены ближе к центру Земли, чем экватор, сила земного тяготения и, следовательно, ускорение свободного падения зависят от географической широты местности. Так на экваторе , а на полюсах .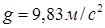

Кроме широты местности ускорение свободного падения зависит от плотности залегающих пород. Поэтому маятниковый прибор можно использовать для обнаружения полезных ископаемых.

В работе используется модель математического маятника – небольшой стальной шарик, свободно подвешенный на длинной, невесомой, нерастяжимой нити.