
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение. Таблица коэффициентов Стьюдента tp,n Количество измерений n Доверительная вероятность p 0,9 0,95 0,98 0,99 0,995 0,997
Таблица коэффициентов Стьюдента tp,n
| Количество измерений n | Доверительная вероятность p | ||||||
| 0,9 | 0,95 | 0,98 | 0,99 | 0,995 | 0,997 | 0,999 | |
| 6,3 | 12,7 | 31,8 | 63,7 | 636,6 | |||
| 2,9 | 4,3 | 7,0 | 9,9 | 31,6 | |||
| 2,4 | 3,2 | 4,5 | 5,8 | 7,4 | 9,3 | 12,9 | |
| 2,1 | 2,8 | 3,7 | 4,6 | 5,6 | 6,8 | 8,6 | |
| 2,0 | 2,6 | 3,4 | 4,0 | 4,7 | 5,8 | 6,9 | |
| 1,9 | 2,4 | 3,1 | 3,7 | 4,3 | 5,0 | 6,0 | |
| 1,9 | 2,4 | 3,0 | 3,5 | 4,0 | 4,6 | 5,4 | |
| 1,9 | 2,3 | 2,9 | 3,4 | 3,8 | 4,3 | 5,0 | |
| 1,8 | 2,3 | 2,8 | 3,3 | 3,7 | 4,2 | 4,8 | |
| 1,8 | 2,2 | 2,7 | 3,2 | 3,6 | 3,6 | 4,6 | |
| 1,7 | 2,1 | 2,5 | 2,9 | 3,3 | 3,4 | 4,1 | |
| 1,7 | 2,0 | 2,5 | 2,8 | 3,2 | 3,3 | 3,8 | |
| 1,7 | 2,0 | 2,5 | 2,7 | 3,0 | 3,2 | 3,6 | |
| 1,7 | 2,0 | 2,4 | 2,7 | 3,0 | 3,2 | 3,5 | |
| 1,6 | 2,0 | 2,4 | 2,7 | 2,9 | 3,2 | 3,4 | |
| 1,6 | 1,98 | 2,4 | 2,62 | 2,85 | 3,1 | 3,37 | |
| ¥ | 1,6 | 1,96 | 2,3 | 2,58 | 2,81 | 3,0 | 3,29 |
Лицензия РБ на издательскую деятельность № 0261 от 10 апреля 1998 г.
Подписано в печать_______________2006 г.
Формат 60х84. Бумага типографская. Гарнитура Таймс.
Усл. печ. л._________. Усл. изд. л.___________
Тираж__________ экз. Заказ № _____________
Издательство Башкирского государственного аграрного университета
Типография Башкирского государственного аграрного университета
Адрес издательства и типографии: 450001, г.Уфа, ул.50 лет Октября,34
МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА
Часть I
Руководство к лабораторным работам по курсу
"Физика, математика"
для студентов специальности "Лечебное дело"
Под редакцией Р.Н. Ростовцева
С.Е. Кажарской
О.В. Шуваевой
Тула
Издательство ТулГУ
УДК 531(076.5)
Механика и молекулярная физика. Часть I. Руководство к лабораторным работам по физике для студентов специальности «Лечебное дело» / под ред. Р.Н. Ростовцева, С.Е. Кажарской, О.В. Шуваевой. Тула: Изд-во ТулГУ, 2012. 62 с.
ISBN
Данное учебно-методическое пособие содержит лабораторные работы по физике, которые будут предложены студентам первого курса специальности «Лечебное дело» в осеннем семестре.
Каждая лабораторная работа содержит краткое теоретическое введение с основными понятиями, формулами, формулировками законов, необходимыми для выполнения лабораторной работы и подготовки к ее защите.
Табл.15. Илл. 32. Библиогр.: 4 назв.
Печатается по решению библиотечно-издательского совета Тульского государственного университета
Рецензент: д-р техн. наук, проф. Чуканов А.Н.
Ó Ростовцев Р.Н., Кажарская С.Е.,
Шуваева О.В., 2012
Ó Изд-во ТулГУ, 2012
ISBN
ЛАБОРАТОРНАЯ РАБОТА 1
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ВЕЩЕСТВА
Цель работы:изучить методики: 1) определения плотности различных веществ; 2) точного взвешивания.
Оборудование:штангенциркуль, тела правильной и произвольной формы, аналитические весы, разновесы.
Теоретическое введение
Плотность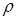 – это масса единицы объема вещества. Для однородного тела плотность постоянна по всему объему V, и масса m равна
– это масса единицы объема вещества. Для однородного тела плотность постоянна по всему объему V, и масса m равна  .
.
Локальная плотность неоднородного тела: 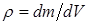 , где dm – масса элементарного объема dV. Тогда
, где dm – масса элементарного объема dV. Тогда 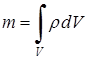 , где
, где 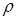 –функция координат.
–функция координат.
Наиболее просто определить плотность тел правильной формы, для которых, измеряя геометрические размеры, легко вычислить объем. Тогда
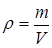 . (1)
. (1)
Если тело неоднородно, то по формуле (1) вычисляют его среднюю плотность.
Массу тела m можно найти, измеряя его вес P = mg . В этом случае
 . (2)
. (2)
 В действительности, формула (2) не точна. Так как взвешивание тела происходит в воздухе, то на него действует дополнительная архимедова сила
В действительности, формула (2) не точна. Так как взвешивание тела происходит в воздухе, то на него действует дополнительная архимедова сила 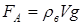 , где
, где 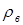 – плотность воздуха (рис. 1). Тогда из условия равновесия
– плотность воздуха (рис. 1). Тогда из условия равновесия

находим
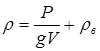 . (3)
. (3)
Воздух при лабораторных условиях можно считать практически идеальным газом с уравнением состояния 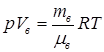 . Поэтому его плотность
. Поэтому его плотность
 , (4)
, (4)
где р и Т – давление и температура воздуха в комнате, 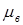 – его молярная масса, R – универсальная газовая постоянная
– его молярная масса, R – универсальная газовая постоянная
(R = 8,31(Дж/(моль×К)).
Так как при изменении температуры меняется и объем взвешиваемого тела (тепловое расширение), и плотность воздуха 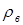 , (но не меняется масса
, (но не меняется масса  тела), то измеряемый вес будет чувствителен к изменению температуры. Поэтому все измерения следует проводить при одной температуре и, желательно, при одинаковой влажности воздуха.
тела), то измеряемый вес будет чувствителен к изменению температуры. Поэтому все измерения следует проводить при одной температуре и, желательно, при одинаковой влажности воздуха.
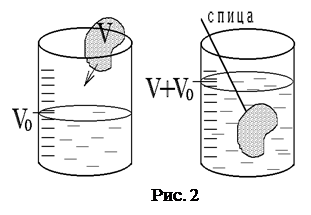 Объем тел неправильной формы можно определить с помощью мензурки, содержащей любую жидкость, погружая в нее исследуемое тело (рис. 2). Если тело плавает в жидкости и не тонет, то его надо полностью погрузить в жидкость с помощью тонкой иглы или спицы.
Объем тел неправильной формы можно определить с помощью мензурки, содержащей любую жидкость, погружая в нее исследуемое тело (рис. 2). Если тело плавает в жидкости и не тонет, то его надо полностью погрузить в жидкость с помощью тонкой иглы или спицы.
 Но, в том случае, когда плотность
Но, в том случае, когда плотность 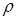 тела больше плотности жидкости, и оно тонет в ней, можно определить плотность, не измеряя объем вытесненной жидкости. Для этого тело взвешивают сначала в воздухе (рис. 1), а потом в жидкости с известной плотностью
тела больше плотности жидкости, и оно тонет в ней, можно определить плотность, не измеряя объем вытесненной жидкости. Для этого тело взвешивают сначала в воздухе (рис. 1), а потом в жидкости с известной плотностью  (например, дистиллированная вода), в которой на тело действует архимедова сила
(например, дистиллированная вода), в которой на тело действует архимедова сила  (рис. 3).
(рис. 3).
Исключая из формулы веса в каждом из двух случаев
 и
и 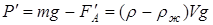
неизвестный объем V,
находим 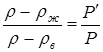 , откуда
, откуда
 . (5)
. (5)
Для определения плотности жидкости  надо взвесить пустой стакан (сосуд), а затем, сняв его с весов, налить в него из мензурки определенный объем жидкости
надо взвесить пустой стакан (сосуд), а затем, сняв его с весов, налить в него из мензурки определенный объем жидкости  и снова взвесить. Зная разность весов
и снова взвесить. Зная разность весов  стакана с жидкостью и без неё, можно по той же формуле (3) вычислить плотность жидкости:
стакана с жидкостью и без неё, можно по той же формуле (3) вычислить плотность жидкости:
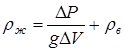 . (6)
. (6)
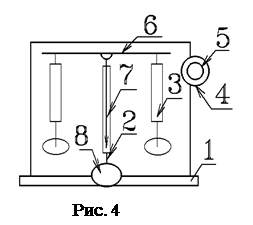 Взвешивают тела на аналитических весах (рис. 4). Весы заключены в витрину, имеющую две открывающиеся боковые дверцы, к основанию 1 прикреплена колонка 2. На колонке укрепляются два кронштейна с воздушными успокоителями-демпферами 3 для ускорения процесса взвешивания. Весы снабжены встроенными в них гирями от 10 до 999 мг. Управление гирями производится с помощью вращающихся лимбов 4 и 5. При вращении малого лимба 4 происходит накладывание или снятие десятков миллиграмм, при вращении большого лимба 5 – сотен миллиграмм. Вращение лимбов происходит независимо друг от друга. На коромысле 6 весов укрепляется стрелка 7. Движущиеся части весов могут быть приподняты с помощью арретира, который приводится в действие маховиком 8.
Взвешивают тела на аналитических весах (рис. 4). Весы заключены в витрину, имеющую две открывающиеся боковые дверцы, к основанию 1 прикреплена колонка 2. На колонке укрепляются два кронштейна с воздушными успокоителями-демпферами 3 для ускорения процесса взвешивания. Весы снабжены встроенными в них гирями от 10 до 999 мг. Управление гирями производится с помощью вращающихся лимбов 4 и 5. При вращении малого лимба 4 происходит накладывание или снятие десятков миллиграмм, при вращении большого лимба 5 – сотен миллиграмм. Вращение лимбов происходит независимо друг от друга. На коромысле 6 весов укрепляется стрелка 7. Движущиеся части весов могут быть приподняты с помощью арретира, который приводится в действие маховиком 8.
Одной из важных областей применения сил инерции центробежного типа является центрифугирование, то есть процесс разделения неоднородной жидкой суспензии в процессе ее вращения.
Рассмотрим вначале разделение суспензии, содержащей твердые частицы различной плотности, в поле силы тяжести. На каждую частицу действуют силы тяжести Р = mg = rчVg и Архимеда Fа = rжVg, где rч и rж – плотности вещества и жидкости соответственно, V – объем частицы. Под действием результирующей силы
Fg = (rч – rж)Vg
происходит расслоение суспензии: частицы с плотностью, большей по сравнению с жидкостью, тонут, с меньшей – всплывают.
Если значения плотностей rч и rж различаются слабо, то результирующая сила Fg мала и процесс разделения суспензии идет достаточно медленно.
Для ускорения процесса разделения в центрифуге сила тяжести заменяется центробежной силой инерции. Рассмотрим вращающийся рабочий объем центрифуги (рис. 5), полностью заполненный разделяемой суспензией. Выделим элемент объема V жидкости, находящийся на расстоянии r от оси вращения ОО¢. При равномерном вращении с угловой скоростью w этот элемент объема движется по круговой траектории радиусом r и в лабораторной системе отсчета на него действуют следующие силы: сила тяжести, уравновешивающая ее сила Архимеда, а также центростремительная сила Fцс = rжVw2r.


 Эта сила действует со стороны жидкости, окружающей элемент объема V, и направлена к оси вращения. В пробной системе отсчета, привязанной к данному элементу объема, непосредственно на элемент объема V будет действовать также центробежная сила. В случае равномерного вращения Fцб = – Fцс.
Эта сила действует со стороны жидкости, окружающей элемент объема V, и направлена к оси вращения. В пробной системе отсчета, привязанной к данному элементу объема, непосредственно на элемент объема V будет действовать также центробежная сила. В случае равномерного вращения Fцб = – Fцс.
Предположим теперь, что элемент объема V представляет собой частицу суспензии плотностью rч = rж. Если эта частица вращается совместно с жидкостью, то со стороны окружающих частиц жидкости на нее действует та же центростремительная сила Fцс = rжVw2r. Кроме того, в пробной системе отсчета на частицу действует и центробежная сила
Fцб = – rчVw2r.
Если центробежная сила Fцб окажется больше центростремительной силы Fцс, то в инерциальной системе отсчета частица начнет двигаться с ускорением, направленным от оси вращения к стенкам рабочего объема центрифуги. Если, наоборот, центробежная сила окажется меньше центростремительной, то частица будет двигаться в сторону оси вращения.
Таким образом, эффективность процесса сепарации определяется величиной результирующей силы
Fр = (rч – rж)Vw2r,
которая оказывается пропорциональной не только разности плотностей частицы и жидкости, но и угловой скорости вращения центрифуги.
«Ультрацентрифуги» позволяют разделять частицы размером менее 100 нм, взвешенные или растворенные в жидкости.
Дата добавления: 2014-10-31; просмотров: 364; Мы поможем в написании вашей работы!; Нарушение авторских прав |