Бегущие волны описываются [1] волновым уравнением

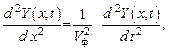
решениями которого [1] для падающей и отраженной волн являются

,

,

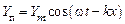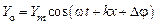где Y_m – амплитуда колебаний частиц струны (амплитуда волны); 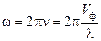– круговая частота, выраженная через частоту колебаний 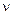, либо через фазовую скорость V_ф и длину бегущей волны l; 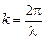– волновое число; х – расстояние, пройденное волной от начала координат за время t; Dj – фазовый сдвиг отраженной волны отно-
сительно волны падающей (Dj зависит от условий на границе отра-
жения).

При суперпозиции падающей и отраженной волн получим стоячую волну

,

где фазовый сдвиг Dj найдем исходя из того, что в точке закрепления струны ее колебания отсутствуют. Так, при х = 0 смещение Y = 0, а это возможно, если 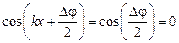, т. е. при Dj = p. Это означает, что падающая и отраженная волны в данной точке струны находятся в противофазе. При суперпозиции образуется стоячая волна, описываемая уравнением

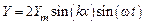. (26.1)

Амплитуда стоячей волны

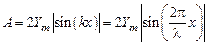
зависит от координаты х и изменяется от А_min = 0 до А_max = 2Y_m
(см. рис. 26.1).

Точки, в которых А = 0, называются узлами стоячей волны. Их координаты х_у получим из условия 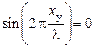, откуда

,

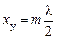где m – 0, 1, 2, 3 ...

Точки, в которых А = А_max = 2Y_m, называются пучностями стоячей волны и, из условия 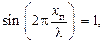имеют координаты

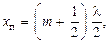
где m = 0, 1, 2, 3 ...

Точки струны, расположенные между двумя узлами, колеблются синфазно, а при переходе через соседний узел фаза их колебаний скачком изменяется на противоположную. Через положение равновесия (ось х) все точки колеблющейся струны проходят одновременно. Расстояние между двумя соседними узлами, равное половине длины бегущих волн, называется длиной стоячей волны 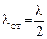(рис. 26.1).

На длине струны может укладываться только целое число длин стоячей волны 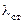, поэтому всегда выполняется условие

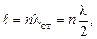
где n = 1, 2, 3 ...

Из этого простого условия следуют важные выводы:.

1. На ограниченной струне стоячая волна может возникать только в том случае, если длина l падающей и отраженной волн равна какому-либо значению из дискретного ряда, разрешенного условием

,

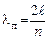где n = 1, 2, 3 ...

2. Колебания ограниченной струны могут происходить только при «собственных частотах», имеющих какое-либо значение из дискретного ряда

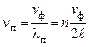, (26.2)

где n = 1, 2, 3 ...

Число n принято называть номером гармоники. Колебания при
n = 1 на частоте

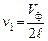(26.3)

называют первой гармоникой (в акустике – основным тоном). Высшие гармоники (в акустике – обертоны) соответствуют n = 2, 3, 4 и т. д.,
т. е. частотам

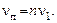
Фазовая скорость V_ф бегущей волны на струне определяется [2] только силой F натяжения струны и её линейной плотностью r

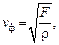(26.4)

причем значение r при известной силе F может быть найдено экспериментально с помощью (26.2) или (26.3).

На рис. 26.2 показаны стоячие волны, соответствующие первым трем гармоникам.

Скорость 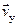(рис. 26.1) различных точек струны в процессе ее колебательного движения найдем, взяв производную по времени от (26.1):

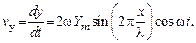
Амплитуда этой скорости

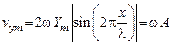
принимает наибольшее значение v_уm(max) в пучности х_п стоячей волны при прохождении струной положения равновесия. Для первой
w₁= 2pv₁гармоники это наибольшее значение скорости струны в точке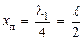

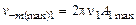. (26.5)

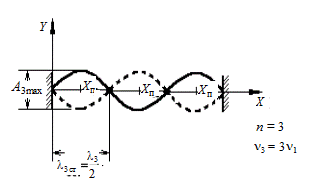
Рис. 26.2

Особенность стоячих волн состоит в том, что они не имеют направления распространения, не переносят энергию колебательного движения. Частицы колеблющейся среды, находящиеся в узлах стоячей волны, всегда покоятся, а координаты узлов во времени и в пространстве не меняются. Остаются постоянными и координаты пучностей.