Будем искать частное решение уравнения

(25.6)

в виде

. (25.7)

Подставляя предполагаемое решение (25.7) в (25.6), получаем

.

Сокращая на и выражая найдем

.

Представим знаменатель этого выражения в показательном виде

.

Модуль этого выражения равен

(25.8)

а аргумент определяется формулой

. (25.9)

Подставляя (25.8) и (25.9) в (25.7), найдем:

и, следовательно,

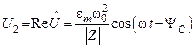. (25.10)

В результате для установившихся вынужденных колебаний напряжения на конденсаторе получаем

, (25.11)

где дает сдвиг фаз между колебаниями напряжения на конденсаторе и колебаниям ЭДС источника.

Из (25.11) видно, что амплитуда вынужденных установившихся колебаний равна

. (25.12)

Величина при (резонансная частота) достигает максимума, который равен

, (25.13)

причем последняя формула верна при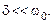

Необходимо отметить (проверьте это самостоятельно), что резонансная частота колебаний напряжения на катушке больше, чем , и, следовательно, резонанс напряжения на LC цепочке наблюдается при промежуточной частоте

.

Уравнение (25.12) определяет форму амплитудно-частотной характеристики (АЧХ) колебаний на конденсаторе, которую называют резонансной кривой (рис. 25.2). Ширина и высота этой кривой зависят от коэффициента Эта величина называется добротностью колебательного контура . Физический смысл этого параметра поясняется в лабораторной работе № 23.

Итак, добротность это

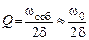. (25.14)

Последнее выражение верно при d << w₀.

Приведем другие выражения для добротности [1, 2]

(25.15)

где l – логарифмический декремент колебаний; R_к – активное сопротивление контура.

Из (25.12) – (25.14) можно получить при w_рез » w₀

. (25.16)

Ширина резонансной кривой зависит, как отмечалось, от добротности контура. При Q >> 1 резонансный максимум оказывается узким, так что в области резонанса

.

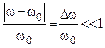В этом случае формула (25.16) принимает более простой вид

. (25.17)

Рис. 25.2

Обычно ширина резонансной кривой 2Dw измеряется на уровне , что соответствует уменьшению мощности колебаний по сравнению с мощностью при резонансе в 2 раза. Подставляя в (25.17) найдем, что ширина резонансной кривой 2Dw на этом уровне и добротность Q связаны соотношением

(25.18)

где n₀= n_С– резонансная частота. Из (25.18) видно, что добротность обратна относительной ширине резонансной кривой.