Характеристика электромагнитных колебаний

Рассмотрим колебательный контур (рис. 23.1). Сопротивление всякого реального контура не равно нулю. Вследствие этого энергия, первоначально запасенная в контуре, непрерывно расходуется на выделение джоулева тепла в сопротивлении R. Поэтому амплитуда электромагнитных колебаний постепенно умень-шается и, в конце концов, они прекращаются. Таким образом, в реальном контуре свободные колебания являются затухающими [1].

Чтобы найти уравнение колебаний в контуре, воспользуемся законом Кирхгофа [2]

, (23.1)

где учтена ЭДС самоиндукции e = e_S.

Выражая в (23.1) напряжения на сопротивлении , на конденсаторе и ЭДС самоиндукции e_Sчерез заряд конденсатора q и параметры контура, получаем дифференциальное уравнение затухающих

колебаний в контуре [2, 3]

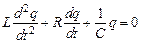. (23.2)

Вводя коэффициент затухания

(23.3)

и обозначая

, (23.4)

где – собственная частота контура, т. е. частота свободных незатухающих колебаний без потерь энергии (при R = 0), уравнение (23.2) можно преобразовать к виду

. (23.5)

Если затухание мало, т. е. < , решение уравнения (23.5) имеет вид

, (23.6)

где

– (23.7)

частота затухающих колебаний в контуре.

Таким образом, при замыкании заряженного конденсатора на цепь из последовательно соединенных L и R, заряд на обкладках конденсатора изменяется с течением времени согласно выражению (23.6). Часто-та затухающих колебаний w определяется параметрами контура R, L, С, причем w < w₀. Если же активное сопротивление контура R = 0, то
w = w₀. Затухающие колебания не являются, строго говоря, периодическим процессом, так как изменяющаяся со временем величина, например, заряд, не принимает одинакового значения через промежуток времени, равный периоду колебаний Т. Тем не менее, в рассматриваемом случае, когда затухание мало, можно говорить о затухающих колебаниях, как о периодических, амплитуда которых постепенно уменьшается по закону 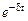(рис. 23.2).

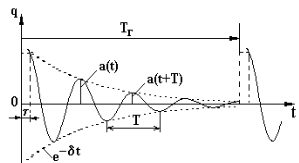
Рис. 23.2